What Is The Lcm Of 24 And 30
News Leon
Mar 21, 2025 · 5 min read
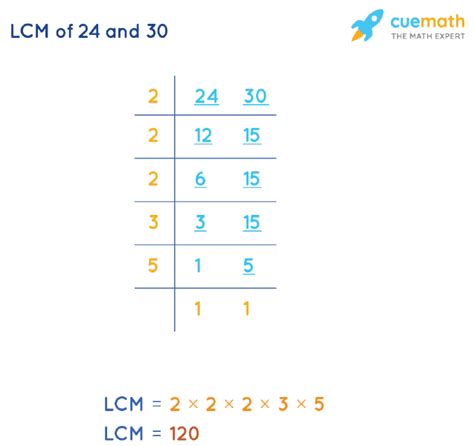
Table of Contents
- What Is The Lcm Of 24 And 30
- Table of Contents
- What is the LCM of 24 and 30? A Deep Dive into Least Common Multiples
- Understanding Least Common Multiples (LCM)
- Method 1: Listing Multiples
- Method 2: Prime Factorization
- Method 3: Using the Greatest Common Divisor (GCD)
- Applications of LCM in Real-World Scenarios
- 1. Scheduling and Timing:
- 2. Fraction Operations:
- 3. Gear Ratios and Mechanical Engineering:
- 4. Music Theory:
- 5. Construction and Engineering:
- Comparing the Methods: Efficiency and Suitability
- Conclusion: The LCM of 24 and 30 and Beyond
- Latest Posts
- Latest Posts
- Related Post
What is the LCM of 24 and 30? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers might seem like a simple mathematical task, especially for smaller numbers like 24 and 30. However, understanding the underlying concepts and various methods for calculating the LCM is crucial for a strong foundation in mathematics and its applications in various fields. This article will delve deep into determining the LCM of 24 and 30, exploring different approaches, and highlighting their significance in practical scenarios.
Understanding Least Common Multiples (LCM)
Before we jump into calculating the LCM of 24 and 30, let's solidify our understanding of what an LCM actually is. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that contains all the numbers as factors.
For example, consider the numbers 2 and 3. Multiples of 2 are 2, 4, 6, 8, 10, 12, and so on. Multiples of 3 are 3, 6, 9, 12, 15, and so on. The common multiples of 2 and 3 are 6, 12, 18, 24, etc. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The most straightforward method, especially for smaller numbers, is to list the multiples of each number until a common multiple is found.
Finding Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
Finding Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240...
By comparing the lists, we can see that the smallest common multiple of 24 and 30 is 120.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 144 and 252 using this method – it would be quite tedious!
Method 2: Prime Factorization
A more efficient and powerful method for finding the LCM involves prime factorization. This method is particularly useful when dealing with larger numbers.
Prime Factorization of 24:
24 = 2 x 2 x 2 x 3 = 2³ x 3¹
Prime Factorization of 30:
30 = 2 x 3 x 5 = 2¹ x 3¹ x 5¹
Calculating the LCM using Prime Factorization:
- Identify the highest power of each prime factor present in the factorizations.
- Multiply these highest powers together.
In our case:
- The highest power of 2 is 2³ = 8
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
Therefore, the LCM(24, 30) = 2³ x 3 x 5 = 8 x 3 x 5 = 120
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and the greatest common divisor (GCD) of two numbers are intimately related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers themselves. This relationship can be expressed as:
LCM(a, b) x GCD(a, b) = a x b
Where 'a' and 'b' are the two numbers.
First, let's find the GCD of 24 and 30 using the Euclidean algorithm:
- 30 = 24 x 1 + 6
- 24 = 6 x 4 + 0
The last non-zero remainder is 6, so the GCD(24, 30) = 6.
Now, we can use the relationship between LCM and GCD:
LCM(24, 30) = (24 x 30) / GCD(24, 30) = (24 x 30) / 6 = 720 / 6 = 120
Applications of LCM in Real-World Scenarios
The concept of LCM isn't just a theoretical mathematical exercise; it has numerous practical applications in various fields:
1. Scheduling and Timing:
Imagine two buses depart from the same station at different intervals. One bus departs every 24 minutes, and the other every 30 minutes. To find out when both buses will depart together again, we need to find the LCM of 24 and 30. The LCM, 120 minutes (or 2 hours), tells us that both buses will depart simultaneously after 2 hours.
2. Fraction Operations:
Finding a common denominator when adding or subtracting fractions requires finding the LCM of the denominators. For instance, to add 1/24 and 1/30, we need to find the LCM of 24 and 30 (which is 120), making the calculation (5/120) + (4/120) = 9/120.
3. Gear Ratios and Mechanical Engineering:
In mechanical systems with gears, LCM plays a crucial role in calculating gear ratios and determining the speed and torque relationships between different components.
4. Music Theory:
LCM is used in music theory to determine the least common multiple of the frequencies of two notes, which helps in understanding harmony and intervals.
5. Construction and Engineering:
In construction and engineering, LCM is used in situations requiring precise measurements and aligning different elements of a structure or system.
Comparing the Methods: Efficiency and Suitability
Each method presented has its strengths and weaknesses:
-
Listing Multiples: Simple for small numbers but highly inefficient for larger numbers.
-
Prime Factorization: Efficient for all sizes of numbers, but requires knowledge of prime factorization.
-
GCD Method: Efficient for larger numbers, but requires calculating the GCD first.
The choice of method depends on the numbers involved and the individual's mathematical skills and preferences. For small numbers, listing multiples might suffice. For larger numbers, prime factorization or the GCD method is generally preferred for efficiency.
Conclusion: The LCM of 24 and 30 and Beyond
Through three distinct methods, we've conclusively determined that the least common multiple of 24 and 30 is 120. This seemingly simple calculation underscores the importance of understanding the fundamental concepts of number theory and the various techniques available for solving mathematical problems. The ability to efficiently calculate LCMs is not merely an academic exercise; it's a practical skill applicable to numerous real-world scenarios, emphasizing the interconnectedness of mathematics and the physical world. Mastering these techniques provides a strong foundation for tackling more complex mathematical challenges in various fields. Understanding LCMs opens doors to a deeper appreciation of mathematical principles and their significant role in our everyday lives.
Latest Posts
Latest Posts
-
How Many Moles Are In 25 Grams Of Water
Mar 28, 2025
-
During Refraction Of Light Through The Glass Slab
Mar 28, 2025
-
The Si Unit Of Resistance Is The
Mar 28, 2025
-
Who Developed Planetary Model Of The Atom
Mar 28, 2025
-
How Many Oxygen Can Hemoglobin Carry
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 24 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
