During Refraction Of Light Through The Glass Slab
News Leon
Mar 28, 2025 · 6 min read
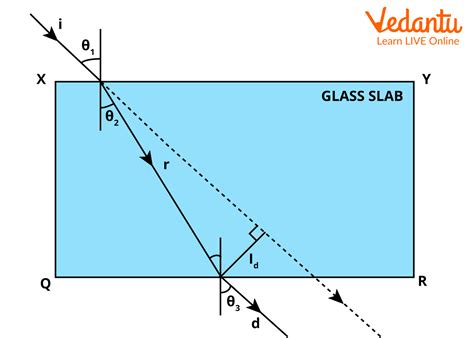
Table of Contents
Refraction of Light Through a Glass Slab: A Deep Dive
Understanding refraction is crucial to grasping the fundamentals of optics. While the concept itself might seem straightforward, the nuances of light's behavior when passing through different mediums, particularly a glass slab, reveal fascinating intricacies. This comprehensive guide delves into the phenomenon of light refraction through a glass slab, exploring its underlying principles, mathematical representation, and real-world applications.
What is Refraction?
Refraction is the bending of light as it passes from one medium to another. This bending occurs because light travels at different speeds in different mediums. When light moves from a less dense medium (like air) to a denser medium (like glass), its speed decreases, causing it to bend towards the normal (an imaginary line perpendicular to the surface at the point of incidence). Conversely, when light moves from a denser medium to a less dense medium, its speed increases, and it bends away from the normal. The extent of this bending is determined by the refractive indices of the two media.
Refractive Index: The Key Player
The refractive index (n) of a medium is a dimensionless number that describes how fast light travels through that medium relative to its speed in a vacuum. A higher refractive index indicates that light travels slower in that medium. The refractive index of air is approximately 1.00, while the refractive index of common glass is around 1.5. This difference in refractive indices is the fundamental reason why light bends when passing through a glass slab.
Snell's Law: Quantifying Refraction
Snell's Law is a fundamental principle in optics that governs the relationship between the angles of incidence and refraction. It states:
n₁sinθ₁ = n₂sinθ₂
Where:
- n₁ is the refractive index of the first medium.
- θ₁ is the angle of incidence (the angle between the incident ray and the normal).
- n₂ is the refractive index of the second medium.
- θ₂ is the angle of refraction (the angle between the refracted ray and the normal).
This equation accurately predicts the direction of the refracted ray given the refractive indices of the two media and the angle of incidence.
Refraction Through a Glass Slab: A Step-by-Step Analysis
Let's consider a ray of light passing through a rectangular glass slab. The process can be broken down into several key stages:
-
Incident Ray: The light ray approaches the glass slab from a less dense medium (typically air) at a certain angle of incidence (θ₁).
-
Refraction at the First Surface: As the light ray enters the glass slab, it slows down and bends towards the normal. The angle of refraction (θ₂) is determined by Snell's Law.
-
Transmission Through the Slab: The light ray continues to travel through the glass slab at a constant angle, provided the slab has parallel faces.
-
Refraction at the Second Surface: As the light ray emerges from the glass slab and re-enters the air, it speeds up and bends away from the normal.
-
Emergent Ray: The final ray, known as the emergent ray, is parallel to the incident ray but laterally displaced. This lateral displacement is a crucial characteristic of light refraction through a glass slab. It's important to note that the emergent ray is parallel to the incident ray only if the slab has parallel faces. If the faces are not parallel, the emergent ray will not be parallel to the incident ray.
Lateral Displacement: A Key Observation
The lateral displacement (d) is the perpendicular distance between the incident and emergent rays. This displacement depends on several factors:
- Thickness of the slab (t): A thicker slab results in a larger lateral displacement.
- Refractive index of the glass (n): A higher refractive index leads to a greater displacement.
- Angle of incidence (θ₁): The displacement is maximum when the angle of incidence is 45 degrees. At normal incidence (θ₁ = 0), there is no lateral displacement.
Mathematical Derivation of Lateral Displacement
The lateral displacement (d) can be derived using simple geometry and Snell's Law. While the full derivation involves trigonometric functions, the essence is capturing the geometric relationship between the incident, refracted, and emergent rays within the context of the slab's thickness and refractive index. The formula typically includes terms involving the thickness of the slab, the refractive index, and the sine of the angles of incidence and refraction.
Applications of Refraction Through a Glass Slab
The principle of refraction through a glass slab, seemingly simple, has far-reaching applications across various fields:
-
Optical Instruments: From microscopes to telescopes, many optical instruments rely on precisely controlled refraction through lenses and prisms (which are essentially multiple glass slabs). These instruments use the refractive properties of glass to magnify, focus, and manipulate light for better image formation.
-
Fiber Optics: Fiber optic cables utilize the principle of total internal reflection, a phenomenon closely related to refraction. Light signals travel long distances through these cables with minimal loss due to the repeated refraction and reflection within the fiber's core.
-
Prisms: Prisms, composed of multiple glass slabs, are used to disperse white light into its constituent colors. This phenomenon is based on the fact that different colors of light have slightly different refractive indices in glass, leading to different bending angles.
-
Spectacles: Spectacles correct refractive errors in the eye by using lenses to refract light appropriately before it reaches the retina. The lenses compensate for problems like myopia (nearsightedness) and hyperopia (farsightedness) ensuring clear vision.
Beyond the Basics: Exploring Advanced Concepts
The phenomenon of refraction through a glass slab forms the bedrock of understanding more complex optical concepts:
-
Total Internal Reflection: When light travels from a denser to a less dense medium, the angle of refraction is always greater than the angle of incidence. At a certain angle of incidence (critical angle), the angle of refraction becomes 90 degrees. Beyond this critical angle, total internal reflection occurs, and the light is reflected back into the denser medium. This principle is fundamental to fiber optics.
-
Dispersion: The dependence of the refractive index on the wavelength of light leads to the phenomenon of dispersion, where different colors of light bend at slightly different angles. This effect is responsible for the separation of white light into its constituent colors by a prism.
-
Polarization: Polarization is the orientation of the light wave's electric field. Refraction can influence the polarization of light, especially when the light passes through anisotropic materials (materials with different refractive indices in different directions).
Conclusion: Refraction – A Cornerstone of Optics
Refraction of light through a glass slab, while a seemingly simple phenomenon, is a cornerstone of optics, driving numerous applications in everyday life and cutting-edge technologies. Understanding Snell's Law, lateral displacement, and the interplay of refractive indices is crucial for comprehending the behavior of light and its manipulation in various optical systems. From the simple act of correcting vision with eyeglasses to the complex workings of fiber optic communication networks, the principles discussed here are instrumental in shaping our understanding and harnessing the power of light. Continued exploration of these concepts unlocks a deeper appreciation for the elegance and precision of optics.
Latest Posts
Latest Posts
-
Which Statement About Equations And Expressions Is True
Mar 31, 2025
-
Points On The Same Line Are Called
Mar 31, 2025
-
Are Tsunami Waves Transverse Or Longitudinal
Mar 31, 2025
-
How To Balance A Nuclear Equation
Mar 31, 2025
-
What Happens To Voltage If Resistance Increases
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about During Refraction Of Light Through The Glass Slab . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
