How To Balance A Nuclear Equation
News Leon
Mar 31, 2025 · 7 min read
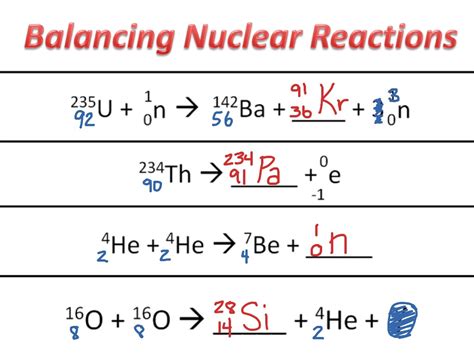
Table of Contents
- How To Balance A Nuclear Equation
- Table of Contents
- How to Balance a Nuclear Equation: A Comprehensive Guide
- Understanding the Basics of Nuclear Equations
- Key Components of a Nuclear Equation
- The Fundamental Principle: Conservation Laws
- 1. Conservation of Mass Number (A):
- 2. Conservation of Atomic Number (Z):
- Step-by-Step Guide to Balancing Nuclear Equations
- Examples of Balancing Nuclear Equations
- Advanced Considerations: Nuclear Fission and Fusion
- Practical Applications and Significance
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
How to Balance a Nuclear Equation: A Comprehensive Guide
Balancing nuclear equations might seem daunting at first, but with a systematic approach and a solid understanding of the fundamental principles, it becomes a manageable and even enjoyable process. This comprehensive guide will equip you with the knowledge and tools to confidently balance any nuclear equation, from simple decay processes to complex nuclear reactions.
Understanding the Basics of Nuclear Equations
Before diving into the balancing process, let's establish a firm foundation in the underlying concepts. Nuclear equations represent the transformations of atomic nuclei, involving changes in the number of protons and neutrons. Unlike chemical equations that focus on electron rearrangement, nuclear equations deal with the fundamental building blocks of matter.
Key Components of a Nuclear Equation
A nuclear equation consists of the following:
-
Nuclides: These are represented by the symbol
<sup>A</sup><sub>Z</sub>X, where:Xis the chemical symbol of the element.Zis the atomic number (number of protons).Ais the mass number (number of protons + neutrons).
-
Reaction Arrows: These indicate the direction of the nuclear transformation.
-
Particles: Various particles can be involved in nuclear reactions, including:
- Alpha particles (α): <sup>4</sup><sub>2</sub>He (2 protons, 2 neutrons)
- Beta particles (β⁻): <sup>0</sup><sub>-1</sub>e (electron)
- Positrons (β⁺): <sup>0</sup><sub>1</sub>e (anti-electron)
- Neutrons (n): <sup>1</sup><sub>0</sub>n
- Protons (p): <sup>1</sup><sub>1</sub>p
- Gamma rays (γ): <sup>0</sup><sub>0</sub>γ (high-energy photons)
The Fundamental Principle: Conservation Laws
The cornerstone of balancing nuclear equations is the principle of conservation. Two fundamental laws must be obeyed:
1. Conservation of Mass Number (A):
The total mass number on the reactant side (left-hand side) must equal the total mass number on the product side (right-hand side) of the equation. This reflects the conservation of nucleons (protons and neutrons).
2. Conservation of Atomic Number (Z):
The total atomic number on the reactant side must equal the total atomic number on the product side. This ensures the conservation of charge.
Step-by-Step Guide to Balancing Nuclear Equations
Let's break down the process with a step-by-step approach, using examples to illustrate each concept:
Step 1: Identify the Unknown
Often, nuclear equations will have one or more unknowns. Your first step is to identify these unknowns, represented by a question mark or an incomplete nuclide symbol.
Step 2: Apply the Conservation Laws
This is the core of balancing. Use the conservation of mass number (A) and the conservation of atomic number (Z) to determine the values of the unknown nuclides.
Step 3: Verify the Balanced Equation
Once you've filled in the blanks, double-check that both mass numbers and atomic numbers are conserved on both sides of the equation.
Examples of Balancing Nuclear Equations
Let's work through several examples, ranging in complexity:
Example 1: Alpha Decay of Uranium-238
Uranium-238 undergoes alpha decay. Write the balanced nuclear equation.
Solution:
-
Reactant: <sup>238</sup><sub>92</sub>U
-
Product: We know it undergoes alpha decay, emitting an alpha particle (<sup>4</sup><sub>2</sub>He). Let's represent the unknown product as <sup>A</sup><sub>Z</sub>X.
The equation becomes:
<sup>238</sup><sub>92</sub>U → <sup>4</sup><sub>2</sub>He + <sup>A</sup><sub>Z</sub>X
- Apply Conservation Laws:
- Conservation of mass number (A): 238 = 4 + A => A = 234
- Conservation of atomic number (Z): 92 = 2 + Z => Z = 90
-
Identify the Product: An element with atomic number 90 is Thorium (Th). Therefore, the product is <sup>234</sup><sub>90</sub>Th.
-
Balanced Equation: <sup>238</sup><sub>92</sub>U → <sup>4</sup><sub>2</sub>He + <sup>234</sup><sub>90</sub>Th
Example 2: Beta Decay of Carbon-14
Carbon-14 undergoes beta decay. Write the balanced nuclear equation.
Solution:
-
Reactant: <sup>14</sup><sub>6</sub>C
-
Product: Beta decay involves the emission of a beta particle (<sup>0</sup><sub>-1</sub>e). The unknown product is <sup>A</sup><sub>Z</sub>X.
The equation becomes:
<sup>14</sup><sub>6</sub>C → <sup>0</sup><sub>-1</sub>e + <sup>A</sup><sub>Z</sub>X
- Apply Conservation Laws:
- Conservation of mass number (A): 14 = 0 + A => A = 14
- Conservation of atomic number (Z): 6 = -1 + Z => Z = 7
-
Identify the Product: An element with atomic number 7 is Nitrogen (N). Therefore, the product is <sup>14</sup><sub>7</sub>N.
-
Balanced Equation: <sup>14</sup><sub>6</sub>C → <sup>0</sup><sub>-1</sub>e + <sup>14</sup><sub>7</sub>N
Example 3: Neutron Capture by Uranium-235
Uranium-235 captures a neutron. Write the balanced equation.
Solution:
-
Reactants: <sup>235</sup><sub>92</sub>U and <sup>1</sup><sub>0</sub>n
-
Product: Let the unknown product be <sup>A</sup><sub>Z</sub>X
The equation becomes:
<sup>235</sup><sub>92</sub>U + <sup>1</sup><sub>0</sub>n → <sup>A</sup><sub>Z</sub>X
- Apply Conservation Laws:
- Conservation of mass number (A): 235 + 1 = A => A = 236
- Conservation of atomic number (Z): 92 + 0 = Z => Z = 92
-
Identify the Product: The product is still Uranium, but with a mass number of 236.
-
Balanced Equation: <sup>235</sup><sub>92</sub>U + <sup>1</sup><sub>0</sub>n → <sup>236</sup><sub>92</sub>U
Example 4: A More Complex Reaction
Consider the reaction: <sup>235</sup><sub>92</sub>U + <sup>1</sup><sub>0</sub>n → <sup>139</sup><sub>56</sub>Ba + <sup>94</sup><sub>36</sub>Kr + x<sup>1</sup><sub>0</sub>n
Determine the value of 'x' (number of neutrons produced).
Solution:
-
Apply Conservation of Mass Number: 235 + 1 = 139 + 94 + x(1) => 236 = 233 + x => x = 3
-
Apply Conservation of Atomic Number: 92 + 0 = 56 + 36 + x(0) => 92 = 92 (This is already balanced)
Therefore, the balanced equation is: <sup>235</sup><sub>92</sub>U + <sup>1</sup><sub>0</sub>n → <sup>139</sup><sub>56</sub>Ba + <sup>94</sup><sub>36</sub>Kr + 3<sup>1</sup><sub>0</sub>n
Advanced Considerations: Nuclear Fission and Fusion
The principles discussed above apply to all nuclear reactions, including the more complex processes of nuclear fission and fusion.
Nuclear Fission: This involves the splitting of a heavy nucleus into two lighter nuclei, often accompanied by the release of neutrons and a significant amount of energy. Balancing fission equations requires careful consideration of all products, including isotopes and emitted particles.
Nuclear Fusion: This involves the combining of two light nuclei into a heavier nucleus, also releasing substantial energy. Fusion reactions often involve isotopes of hydrogen, resulting in the formation of helium and other products. Again, meticulous application of conservation laws is essential.
Practical Applications and Significance
Balancing nuclear equations is not just an academic exercise. It's a crucial skill in various fields:
- Nuclear Medicine: Understanding nuclear decay is critical in developing and using radioisotopes for diagnostic and therapeutic purposes.
- Nuclear Engineering: Accurate calculations are essential for designing and operating nuclear reactors safely and efficiently.
- Nuclear Physics Research: Balancing equations is fundamental to analyzing experimental data and advancing our understanding of nuclear processes.
- Nuclear Forensics: Tracing the origin and nature of nuclear materials requires a deep understanding of nuclear reactions and decay chains.
Conclusion
Balancing nuclear equations is a fundamental skill in nuclear science and related fields. By mastering the principles of conservation of mass number and atomic number, and following a systematic approach, you can confidently tackle even the most complex nuclear reactions. This understanding forms the basis for numerous applications, ranging from medical treatments to the development of sustainable energy sources. Continuous practice and engagement with diverse examples will solidify your understanding and build your confidence in this essential area of scientific study.
Latest Posts
Latest Posts
-
Dna Serves As A Template For The Synthesis Of
Apr 03, 2025
-
Ice Has Lower Density Than Water Because Ice
Apr 03, 2025
-
Hcl Ca Oh 2 H2o Cacl2
Apr 03, 2025
-
Is Tap Water A Pure Substance Or Mixture
Apr 03, 2025
-
A Particle Can Slide Along A Track With Elevated
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How To Balance A Nuclear Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
