Points On The Same Line Are Called
News Leon
Mar 31, 2025 · 6 min read
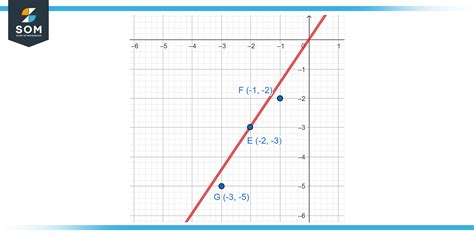
Table of Contents
Points on the Same Line are Called Collinear Points: A Deep Dive into Geometry
Understanding the fundamental concepts of geometry is crucial for success in mathematics and various STEM fields. One such fundamental concept is collinearity, which describes the relationship between points lying on the same straight line. This article delves deep into the definition of collinear points, exploring various methods to determine collinearity, its applications in different areas of mathematics, and its significance in advanced geometrical concepts.
Defining Collinear Points: A Straightforward Explanation
In geometry, collinear points are defined as two or more points that lie on the same straight line. No matter how many points are involved, as long as a single straight line can pass through all of them, they are considered collinear. If you can draw a line that perfectly connects all the points without needing to change direction, those points are collinear. The simplest example is any two points; they are always collinear because you can always draw a single line connecting them. However, three or more points might or might not be collinear.
Methods for Determining Collinearity
Several methods can be employed to determine whether a set of points is collinear. The most common methods involve:
1. Visual Inspection (For Simple Cases):
For a small number of points plotted on a graph, visual inspection can suffice. If the points appear to lie on a single straight line, they are likely collinear. However, this method is unreliable for complex cases or when dealing with a large number of points with close proximity. It is prone to human error and subjective interpretation.
2. Slope Calculation (For Two or More Points):
The slope of a line is a measure of its steepness. If two or more points are collinear, the slope between any pair of points will be the same. Let's consider two points, A(x₁, y₁) and B(x₂, y₂). The slope (m) is calculated as:
m = (y₂ - y₁) / (x₂ - x₁)
If you calculate the slope between multiple pairs of points from a set, and they all yield the same slope, then the points are collinear. However, it is important to note that this method struggles with vertical lines (where x₁ = x₂), as the slope becomes undefined.
3. Area of a Triangle Method (For Three Points):
Consider three points, A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃). These three points can be used to define a triangle. The area of this triangle can be calculated using the determinant formula:
Area = 0.5 * |x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂)|
If the points are collinear, the area of the triangle formed by them will be zero. This is because the triangle degenerates into a straight line. This method is particularly useful for determining collinearity of three points and forms a robust basis for extending to more points.
4. Using the Equation of a Line:
If you have the equation of a line (in the form y = mx + c, or Ax + By + C = 0), you can simply substitute the coordinates of each point into the equation. If the equation holds true for all points, then the points are collinear. This method is powerful because it allows for direct verification against a known line.
5. Vector Approach (For Three or More Points):
Vectors provide another elegant approach to determine collinearity. Consider three points A, B, and C. If the vectors AB and AC are parallel (i.e., one is a scalar multiple of the other), then the points are collinear. This is because parallel vectors indicate that the points lie on the same line. Mathematically, this means:
AB = k * AC where k is a scalar.
Applications of Collinearity
The concept of collinearity isn't just a theoretical exercise; it finds practical applications in various fields:
1. Computer Graphics and Computer-Aided Design (CAD):
Collinearity is crucial in computer graphics for tasks such as line clipping, polygon simplification, and collision detection. Determining if vertices of a polygon are collinear allows for optimization and efficient rendering. CAD software heavily relies on these algorithms for precise geometric modeling.
2. Surveying and Mapping:
Surveyors use collinearity to check the accuracy of their measurements and ensure that points are correctly aligned. The principle is used in establishing control points and creating accurate maps and plans.
3. Physics and Engineering:
In mechanics and structural analysis, determining if points are collinear is essential for analyzing forces, stresses, and stability of structures. The concept plays a vital role in calculating moments and determining the equilibrium of systems.
4. Image Processing:
In image processing and computer vision, collinearity is used for feature detection and object recognition. Identifying collinear features in images can be beneficial for simplifying object representations and improving efficiency in processing visual data.
5. Cryptography:
In certain cryptographic algorithms, collinearity tests can be used for authentication and security purposes.
Extending Collinearity to Higher Dimensions
The concept of collinearity can be generalized to higher dimensions. In three-dimensional space, collinear points are defined as points that lie on the same straight line. The methods described earlier can be adapted to three dimensions, using vector techniques and equations of lines in 3D space. In higher dimensions, collinearity corresponds to points lying on the same straight line, although visualizing it becomes more challenging.
Significance in Advanced Geometrical Concepts
Collinearity plays a crucial role in many advanced geometrical concepts. For instance:
1. Concurrency:
In geometry, concurrency is the property of lines intersecting at a single point. Determining if lines are concurrent often involves checking for collinearity of points of intersection.
2. Perspective Geometry:
Collinearity is a fundamental concept in projective geometry, used in understanding perspective transformations and the mapping of points from one plane to another.
3. Menelaus' Theorem:
Menelaus' Theorem is a classic theorem in geometry that deals with collinearity of points on the sides of a triangle. This theorem provides a condition for three points on the sides of a triangle to be collinear.
Conclusion: The Ubiquitous Nature of Collinearity
Collinearity, a seemingly simple geometrical concept, holds profound importance and wide-ranging applications across various fields. Understanding how to determine if points are collinear is essential for mastering many aspects of mathematics, computer science, and engineering. From basic geometry problems to advanced algorithms and theoretical frameworks, the concept of collinearity remains a fundamental building block. The various methods presented here offer a comprehensive toolkit for effectively tackling collinearity in diverse contexts. As we continue to advance in technology and scientific understanding, the significance of this seemingly basic concept will only continue to grow.
Latest Posts
Latest Posts
-
Every Integer Is A Real Number
Apr 01, 2025
-
Count Vowels In A String Python
Apr 01, 2025
-
Which Of The Following Elements Is Most Electronegative
Apr 01, 2025
-
For Which Value Of X Is Abcd A Kite
Apr 01, 2025
-
64 To The Power Of 1 2
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Points On The Same Line Are Called . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
