Every Integer Is A Real Number
News Leon
Apr 01, 2025 · 5 min read
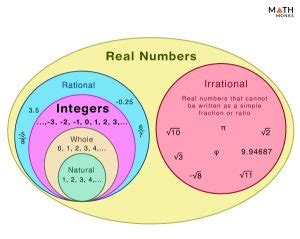
Table of Contents
Every Integer is a Real Number: A Deep Dive into Number Systems
The statement "every integer is a real number" might seem self-evident, almost trivially true. However, a deeper understanding of number systems reveals a rich tapestry of mathematical relationships, and appreciating this seemingly simple statement requires exploring the hierarchical structure of numbers. This article will delve into the various number sets, highlighting the inclusion of integers within the real numbers and examining the implications of this relationship. We will explore the concepts with examples and address potential misunderstandings.
Understanding Number Systems: A Hierarchical View
Before we definitively state that every integer is a real number, let's establish a clear understanding of the different number sets involved. The number systems form a nested hierarchy, with each set encompassing its predecessors.
1. Natural Numbers (ℕ): The Counting Numbers
The most basic set is the natural numbers, also known as counting numbers. These are the numbers we use to count objects: 1, 2, 3, 4, and so on. They are positive whole numbers, excluding zero. This set is denoted by ℕ.
Example: The number of apples in a basket, the number of students in a classroom.
2. Whole Numbers (ℤ₀): Adding Zero
Adding zero to the natural numbers creates the set of whole numbers, denoted by ℤ₀ (sometimes also represented as ℕ₀). This set includes all natural numbers and zero.
Example: The number of cars in a parking lot (which could be zero), the balance in a bank account (potentially zero).
3. Integers (ℤ): Introducing Negative Numbers
Expanding further, we introduce negative numbers to the whole numbers, creating the set of integers, denoted by ℤ. Integers include all positive and negative whole numbers, and zero.
Example: Temperatures above and below zero, elevations above and below sea level, profits and losses in a business.
4. Rational Numbers (ℚ): Fractions and Decimals
The rational numbers, denoted by ℚ, represent a significant leap in complexity. This set includes all numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. This means that rational numbers include all integers (as they can be expressed as p/1) as well as fractions and terminating or repeating decimals.
Example: 1/2, 3/4, -2/5, 0.75, 0.333... (1/3)
5. Irrational Numbers (𝕀): The Non-Repeating, Non-Terminating Decimals
Irrational numbers, denoted by 𝕀, are numbers that cannot be expressed as a fraction of two integers. These numbers have decimal representations that are non-terminating and non-repeating. This means their decimal expansions go on forever without exhibiting any repeating pattern.
Example: π (pi) ≈ 3.14159265..., √2 ≈ 1.41421356..., e (Euler's number) ≈ 2.71828...
6. Real Numbers (ℝ): The Union of Rational and Irrational Numbers
Finally, we arrive at the real numbers, denoted by ℝ. This set encompasses all rational and irrational numbers. Essentially, real numbers represent all numbers that can be plotted on a number line.
Example: All the examples from the previous sets (integers, rational numbers, and irrational numbers) are all part of the real number set.
The Definitive Proof: Every Integer is a Real Number
Now, armed with a comprehensive understanding of these number sets, we can formally establish the truth of the statement: every integer is a real number.
The reasoning is straightforward:
-
Integers are rational numbers: Every integer n can be expressed as the fraction n/1. Since n and 1 are both integers, and 1 is not zero, every integer satisfies the definition of a rational number.
-
Rational numbers are real numbers: The real number set is defined as the union of rational and irrational numbers. Since rational numbers are a subset of real numbers, every rational number is also a real number.
-
Therefore, integers are real numbers: By the transitive property (if A is a subset of B, and B is a subset of C, then A is a subset of C), we conclude that since integers are rational numbers, and rational numbers are real numbers, then integers are real numbers.
This simple logical progression demonstrates the inclusive nature of the real number system. The real numbers encompass all the previously discussed number sets, making the statement "every integer is a real number" undeniably true.
Implications and Applications
Understanding the relationship between integers and real numbers is fundamental to many areas of mathematics and its applications. Here are a few examples:
-
Calculus: Calculus extensively uses real numbers, including integers, in its operations. Derivatives and integrals often involve calculations with integer values, especially when dealing with discrete functions or approximating continuous functions.
-
Linear Algebra: Vectors and matrices often contain integer elements, which are treated within the framework of real number arithmetic.
-
Computer Science: While computers often work with discrete representations of numbers, the underlying mathematical principles frequently rely on the properties of real numbers, including integers, to design and analyze algorithms.
-
Physics and Engineering: Many physical quantities, such as mass, charge, or temperature, are often modeled using real numbers, even when measurements provide only integer values. This allows for a more precise and accurate representation of the physical system.
Addressing Potential Misconceptions
Occasionally, there might be a confusion regarding the difference between real numbers and integers. This often stems from focusing solely on the decimal representation of numbers. It's crucial to remember that the definition of a number system determines its membership, not merely its visual form.
For instance, the number 5 is an integer. It's also a rational number (5/1) and, consequently, a real number. The fact that its decimal representation is simply "5" doesn't diminish its membership in the broader sets of real numbers.
Conclusion: A Foundation for Further Exploration
This article has provided a thorough exploration of the relationship between integers and real numbers, demonstrating unequivocally that every integer is indeed a real number. Understanding this hierarchical structure of number systems is critical for grasping more advanced mathematical concepts. This foundational knowledge forms the bedrock for exploring fields such as calculus, linear algebra, and various branches of applied mathematics and science. As you progress in your mathematical journey, remembering the inclusive nature of the real number system will prove invaluable in solving problems and understanding complex systems. The seemingly simple statement "every integer is a real number" therefore serves as a gateway to a deeper appreciation of the elegance and interconnectedness of mathematical concepts.
Latest Posts
Latest Posts
-
Why Are Fleas Hard To Squish
Apr 03, 2025
-
How Many Chromosomes In A Daughter Cell
Apr 03, 2025
-
Why Do Bones Heal Quicker Than Cartilage
Apr 03, 2025
-
Can Magnitude Be Negative In Physics
Apr 03, 2025
-
What Is The Area Of Triangle Rst
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Every Integer Is A Real Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
