What Is The Area Of Triangle Rst
News Leon
Apr 03, 2025 · 5 min read
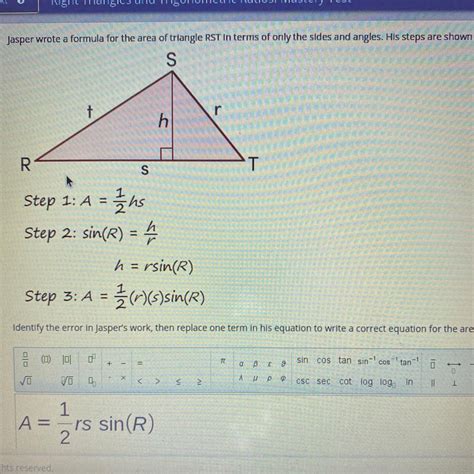
Table of Contents
What is the Area of Triangle RST? A Comprehensive Guide
Finding the area of a triangle is a fundamental concept in geometry, with applications spanning various fields from architecture and engineering to computer graphics and data analysis. While the basic formula—half the base times the height—is well-known, understanding how to apply it effectively, particularly in more complex scenarios involving different types of triangles and given information, requires a deeper dive. This article will provide a comprehensive guide to calculating the area of triangle RST, exploring various methods and addressing common challenges.
Understanding the Basics: The Standard Formula
The most common and widely used formula for the area of any triangle is:
Area = (1/2) * base * height
Where:
- base: Any side of the triangle can be chosen as the base.
- height: The perpendicular distance from the vertex opposite the chosen base to the base itself.
This formula is incredibly versatile, but its practical application depends heavily on the information provided about triangle RST. Let's explore different scenarios.
Scenario 1: Base and Height are Given
This is the simplest scenario. If the length of the base and the corresponding height of triangle RST are known, calculating the area is straightforward.
Example:
Let's say the base of triangle RST (RS) is 10 units and the height (h) from T to RS is 6 units.
Area = (1/2) * 10 * 6 = 30 square units
Scenario 2: Coordinates of Vertices are Given
If we know the coordinates of the vertices R, S, and T in a Cartesian plane, we can use the determinant method to calculate the area. This method utilizes the coordinates (x, y) of each vertex:
Area = (1/2) |(x<sub>R</sub>(y<sub>S</sub> - y<sub>T</sub>) + x<sub>S</sub>(y<sub>T</sub> - y<sub>R</sub>) + x<sub>T</sub>(y<sub>R</sub> - y<sub>S</sub>))|
Where:
- (x<sub>R</sub>, y<sub>R</sub>) are the coordinates of vertex R
- (x<sub>S</sub>, y<sub>S</sub>) are the coordinates of vertex S
- (x<sub>T</sub>, y<sub>T</sub>) are the coordinates of vertex T
The absolute value ensures a positive area. This formula is particularly useful when dealing with triangles defined within a coordinate system.
Example:
Let's say the coordinates are R(1, 2), S(4, 6), and T(7, 2).
Area = (1/2) |(1(6 - 2) + 4(2 - 2) + 7(2 - 6))| = (1/2) |(4 + 0 - 28)| = (1/2) |-24| = 12 square units
Scenario 3: Using Heron's Formula (Sides are Given)
Heron's formula is a powerful tool when the lengths of all three sides of triangle RST are known, but the height is not. This formula uses the concept of the semi-perimeter:
s = (a + b + c) / 2
where a, b, and c are the lengths of the sides. The area is then calculated as:
Area = √(s(s - a)(s - b)(s - c))
This formula is elegant but computationally more intensive than the base-height formula.
Example:
Let's say the sides of triangle RST are a = 5, b = 6, and c = 7.
s = (5 + 6 + 7) / 2 = 9
Area = √(9(9 - 5)(9 - 6)(9 - 7)) = √(9 * 4 * 3 * 2) = √216 ≈ 14.7 square units
Scenario 4: Using Trigonometry (Two Sides and Included Angle)
If we know the lengths of two sides of triangle RST and the angle between them, we can use trigonometry to find the area. This involves the formula:
Area = (1/2) * a * b * sin(C)
Where:
- a and b are the lengths of two sides.
- C is the angle between sides a and b.
Example:
Let's say RS = 8, ST = 6, and the angle ∠RST = 30°.
Area = (1/2) * 8 * 6 * sin(30°) = 24 * (1/2) = 12 square units
Advanced Techniques and Considerations
The methods described above cover the most common scenarios. However, more advanced techniques might be necessary in certain situations:
1. Dealing with Irregular Triangles:
For irregular triangles with no easily identifiable base and height, breaking the triangle into smaller, simpler shapes (like right-angled triangles) can be a useful strategy. Calculate the area of each smaller triangle and sum them to find the total area of triangle RST.
2. Using Calculus for Complex Shapes:
In cases involving curves or complex shapes, integral calculus might be necessary to determine the area. This approach involves integrating the equation of the curve that defines the triangle's boundary.
3. Utilizing Vector Methods:
Vector methods offer a powerful and elegant way to compute areas. The area of a triangle formed by vectors u and v is given by (1/2) ||u x v||, where "x" denotes the cross product and || || represents the magnitude.
Error Handling and Practical Tips
Several potential pitfalls can lead to inaccurate area calculations:
- Incorrect Unit Conversions: Ensure all measurements are in consistent units (e.g., all in meters or all in centimeters).
- Rounding Errors: Minimize rounding errors by carrying extra decimal places during calculations.
- Misinterpretation of Given Information: Carefully read and understand the information provided about triangle RST before selecting the appropriate formula.
Conclusion: Mastering Triangle Area Calculations
Calculating the area of triangle RST, while seemingly straightforward, involves a range of techniques depending on the available information. From the basic base-height formula to the sophisticated Heron's formula and trigonometric approaches, understanding these methods empowers you to tackle a wide variety of geometric problems. By mastering these techniques and understanding potential pitfalls, you can confidently and accurately determine the area of any triangle you encounter, regardless of its shape or the information provided. Remember to always double-check your work and consider the context of the problem to select the most efficient and appropriate method. This thorough understanding will undoubtedly benefit you in various fields where geometrical calculations are crucial.
Latest Posts
Latest Posts
-
What Is A Subatomic Particle With A Positive Charge
Apr 03, 2025
-
Which Of The Following Is True About Sexual Reproduction
Apr 03, 2025
-
Do Noble Gases Have High Ionization Energy
Apr 03, 2025
-
Do Plane Mirrors Form Real Images
Apr 03, 2025
-
After 1880 European Colonization Was Motivated By The
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of Triangle Rst . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
