64 To The Power Of 1/2
News Leon
Apr 01, 2025 · 6 min read
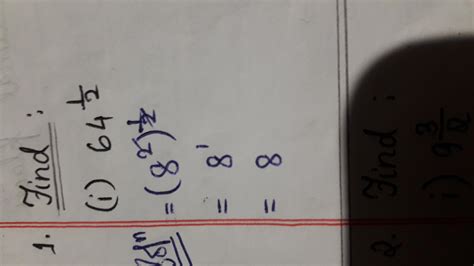
Table of Contents
64 to the Power of 1/2: Unveiling the Secrets of Fractional Exponents
Understanding exponents is fundamental to mathematics, forming the bedrock of many advanced concepts. While working with whole number exponents is relatively straightforward, fractional exponents often present a challenge. This article delves into the meaning and calculation of 64 to the power of 1/2 (64<sup>1/2</sup>), exploring the underlying principles and expanding on the broader context of fractional exponents. We will uncover why this seemingly simple calculation holds significant mathematical importance and how it connects to various areas of study.
What Does 64<sup>1/2</sup> Mean?
The expression 64<sup>1/2</sup> signifies the square root of 64. In simpler terms, it asks: "What number, when multiplied by itself, equals 64?" The fractional exponent 1/2 is a way of representing the square root operation mathematically. This notation extends the concept of exponents beyond whole numbers, allowing us to express roots concisely and consistently within the broader framework of exponential functions.
Understanding Fractional Exponents: A Deeper Dive
A fractional exponent, such as a<sup>m/n</sup>, can be understood in two equivalent ways:
- Root of a Power: It represents the nth root of a raised to the power of m. In other words, a<sup>m/n</sup> = (a<sup>m</sup>)<sup>1/n</sup> = <sup>n</sup>√(a<sup>m</sup>).
- Power of a Root: Alternatively, it represents the mth power of the nth root of a. This means a<sup>m/n</sup> = (<sup>n</sup>√a)<sup>m</sup>.
Both interpretations yield the same result. For 64<sup>1/2</sup>, we have:
- Root of a Power: (64<sup>1</sup>)<sup>1/2</sup> = √64 = 8
- Power of a Root: (√64)<sup>1</sup> = 8<sup>1</sup> = 8
This demonstrates the equivalence and interchangeability of the two interpretations.
Calculating 64<sup>1/2</sup>
Calculating 64<sup>1/2</sup> is a relatively straightforward process. Since we're dealing with the square root, we need to find a number that, when multiplied by itself, gives 64. The answer is 8, because 8 x 8 = 64.
Therefore:
64<sup>1/2</sup> = 8
Beyond the Simple Calculation: Exploring the Implications
While the calculation itself is simple, understanding the underlying principles behind fractional exponents unlocks a world of mathematical possibilities. Let's explore some crucial implications:
-
Connection to Geometry: The square root is intrinsically linked to geometric concepts. For example, if you have a square with an area of 64 square units, the length of its side is 64<sup>1/2</sup> = 8 units. This demonstrates the practical application of fractional exponents in geometric problems.
-
Solving Equations: Fractional exponents are crucial in solving equations involving roots. For instance, an equation like x<sup>2</sup> = 64 can be solved by taking the square root of both sides, leading to x = ±64<sup>1/2</sup> = ±8. The ± symbol highlights the fact that both positive and negative 8 satisfy the equation.
-
Extending Exponential Functions: Fractional exponents seamlessly extend the concept of exponents from whole numbers to rational numbers (fractions). This allows for a more continuous and comprehensive understanding of exponential functions and their properties. For example, we can now plot points on an exponential graph for fractional values of the exponent.
Fractional Exponents and Their Generalizations: A Broader Perspective
The concept of fractional exponents extends far beyond the simple case of 64<sup>1/2</sup>. Consider the general case: a<sup>m/n</sup>. As discussed earlier, this can be interpreted as:
- (a<sup>m</sup>)<sup>1/n</sup> = <sup>n</sup>√(a<sup>m</sup>)
- (<sup>n</sup>√a)<sup>m</sup>
These interpretations apply to a wide range of numbers and are crucial for various mathematical operations and problem-solving scenarios. Understanding this general case allows one to tackle more complex fractional exponents and problems involving them.
Dealing with Negative Fractional Exponents
The concept extends to negative fractional exponents as well. A negative exponent indicates a reciprocal: a<sup>-m/n</sup> = 1 / a<sup>m/n</sup>. For example, 64<sup>-1/2</sup> = 1 / 64<sup>1/2</sup> = 1/8.
Working with Irrational Exponents
While the focus has been on rational exponents (fractions), the concept can also be extended to irrational exponents (like π or √2). These exponents are tackled using limits and calculus, leading to the concept of exponential functions for all real numbers.
Applications of Fractional Exponents in Real-World Scenarios
Fractional exponents are not just abstract mathematical concepts; they have significant practical applications across various disciplines:
-
Physics: Many physical phenomena are modeled using exponential functions with fractional exponents. Examples include the decay of radioactive materials and the damping of oscillations.
-
Engineering: In structural engineering, the calculation of stresses and strains often involves fractional exponents. Understanding these principles is vital for designing safe and reliable structures.
-
Finance: Compound interest calculations use exponential functions, and understanding fractional exponents is crucial for accurate financial modeling.
-
Computer Science: Algorithms and data structures often utilize exponential functions, and understanding the properties of fractional exponents is crucial for optimizing performance.
-
Biology: Exponential growth and decay models are widely used in population dynamics and other biological processes.
Mastering Fractional Exponents: Tips and Practice
Mastering fractional exponents requires consistent practice and a strong understanding of the underlying principles. Here are some helpful tips:
-
Start with the basics: Begin with simple examples, gradually increasing the complexity of the calculations.
-
Understand the different interpretations: Be comfortable with both the "root of a power" and the "power of a root" interpretations of fractional exponents.
-
Practice regularly: Regular practice is key to solidifying your understanding and building confidence.
-
Use online resources: Many online resources, including calculators and tutorials, can help you improve your understanding and skills.
-
Solve problems from different contexts: Apply your knowledge to problems from various fields like geometry, algebra, and physics to gain a deeper comprehension of the concept.
Conclusion: Unlocking the Power of Fractional Exponents
64<sup>1/2</sup>, while seemingly a simple calculation, serves as a gateway to a deeper understanding of fractional exponents. This exploration has revealed the meaning, calculation methods, and broader significance of fractional exponents within the realm of mathematics and its diverse applications in the real world. By grasping the fundamental principles and practicing regularly, one can unlock the power of fractional exponents and utilize them effectively in numerous contexts. Remember that consistent practice and a solid understanding of the underlying concepts are key to mastering this crucial mathematical tool.
Latest Posts
Latest Posts
-
Distance Between Two Parallel Planes Formula
Apr 03, 2025
-
What Particle Determines The Identity Of An Element
Apr 03, 2025
-
Which Statement Is True About Bacteria
Apr 03, 2025
-
Why Are Fleas Hard To Squish
Apr 03, 2025
-
How Many Chromosomes In A Daughter Cell
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about 64 To The Power Of 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
