Distance Between Two Parallel Planes Formula
News Leon
Apr 03, 2025 · 4 min read
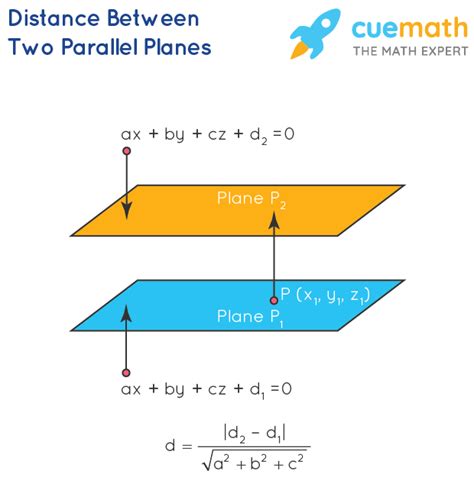
Table of Contents
Distance Between Two Parallel Planes Formula: A Comprehensive Guide
Finding the distance between two parallel planes is a fundamental concept in three-dimensional geometry with applications spanning various fields, including computer graphics, physics, and engineering. This comprehensive guide will explore the formula, its derivation, and practical applications, ensuring a thorough understanding of this important geometric concept.
Understanding Parallel Planes
Before diving into the formula, let's solidify our understanding of parallel planes. Two planes are considered parallel if they never intersect, no matter how far they extend. Think of two perfectly flat sheets of paper stacked on top of each other – they represent parallel planes. The key characteristic is that they maintain a constant distance between them throughout their entire extent.
The Formula: A Concise Explanation
The formula for calculating the distance (d) between two parallel planes is elegantly simple:
d = |D₂ - D₁| / √(A² + B² + C²)
Where:
- D₁ and D₂ are the constant terms in the equations of the two parallel planes (expressed in the standard form Ax + By + Cz + D = 0). Remember that for parallel planes, the coefficients A, B, and C are identical. Only the constant term, D, differs.
- A, B, and C are the coefficients of x, y, and z respectively in the equation of either plane (since they are identical for parallel planes). These coefficients define the orientation of the planes in space.
Step-by-Step Calculation: A Worked Example
Let's illustrate the formula with a concrete example. Consider two parallel planes defined by the following equations:
- Plane 1: 2x + 3y - z + 4 = 0 (D₁ = 4)
- Plane 2: 2x + 3y - z - 6 = 0 (D₂ = -6)
Here's how to calculate the distance between them:
-
Identify A, B, C, D₁ and D₂: From the equations above, we have A = 2, B = 3, C = -1, D₁ = 4, and D₂ = -6.
-
Substitute into the formula: Plug the values into the distance formula:
d = |(-6) - 4| / √(2² + 3² + (-1)²) = |-10| / √(4 + 9 + 1) = 10 / √14
-
Simplify the result: Calculate the square root and divide:
d ≈ 10 / 3.74 ≈ 2.67
Therefore, the distance between the two parallel planes is approximately 2.67 units.
Derivation of the Formula: A Deeper Dive
The formula's derivation involves vector geometry and the concept of normal vectors. Let's break down the process:
-
Normal Vector: Both parallel planes share the same normal vector, n = (A, B, C). The normal vector is perpendicular to the plane.
-
Point on a Plane: Choose any point P₁ on Plane 1. Its coordinates will satisfy the equation of Plane 1.
-
Vector Projection: Construct a vector from P₁ to Plane 2. This vector will be parallel to the normal vector. We can find a point P₂ on Plane 2 and calculate the vector v = P₂ - P₁.
-
Scalar Projection: The distance between the planes is the scalar projection of the vector v onto the normal vector n. This scalar projection is given by:
d = | v • n | / ||n||
where • represents the dot product and || || represents the magnitude (length) of the vector.
-
Simplification: Through algebraic manipulation involving the plane equations and the dot product, the above formula simplifies to the concise form presented earlier:
d = |D₂ - D₁| / √(A² + B² + C²)
Applications in Real-World Scenarios
The distance between parallel planes has numerous practical applications:
-
Computer Graphics: Determining the distance between objects and planes is crucial for collision detection and rendering techniques in 3D graphics.
-
Physics: In mechanics, calculating the distance between parallel plates helps in determining the electric field strength between charged plates or the forces in certain mechanical systems.
-
Engineering: The concept is used in structural engineering for analyzing parallel structural elements, determining clearances, and ensuring safe distances between components.
-
Architectural Design: In architectural modelling and design, this knowledge helps determine precise distances between parallel walls or structural elements in buildings.
-
Robotics: Distance calculations are essential for path planning and obstacle avoidance in robotics. Determining the distance between the robot arm and parallel surfaces is critical for safe and effective operation.
Handling Special Cases and Potential Pitfalls
While the formula is generally straightforward, some scenarios require extra attention:
-
Planes with Different Normal Vectors: The formula only applies to parallel planes. If the planes are not parallel, they will intersect, and the distance between them is undefined.
-
Planes Coinciding: If the equations of the planes are identical except for a constant factor multiplying the whole equation, the planes coincide, and the distance between them is zero.
-
Incorrect Equation Forms: Ensure the plane equations are in the standard form Ax + By + Cz + D = 0 before applying the formula. Any other form needs to be converted first.
Conclusion: Mastering the Distance Calculation
Understanding and applying the formula for the distance between two parallel planes is a cornerstone of spatial reasoning and problem-solving in many fields. By mastering the formula, its derivation, and its applications, you will significantly enhance your ability to approach and resolve geometric problems in diverse contexts. Remember to always check for special cases and ensure your equations are in the correct standard form to prevent inaccuracies. With practice and attention to detail, you'll become adept at confidently calculating the distance between parallel planes.
Latest Posts
Latest Posts
-
Sin X Cos X Sec X
Apr 03, 2025
-
Which Of The Following Is True Regarding The Normal Distribution
Apr 03, 2025
-
How Many Electrons Can P Orbital Hold
Apr 03, 2025
-
Genetic Information Is Encoded In The
Apr 03, 2025
-
A Photocell Operates On Which Photoelectric Effect
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Distance Between Two Parallel Planes Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
