The Total Momentum Of A System Is Conserved __________.
News Leon
Apr 05, 2025 · 6 min read
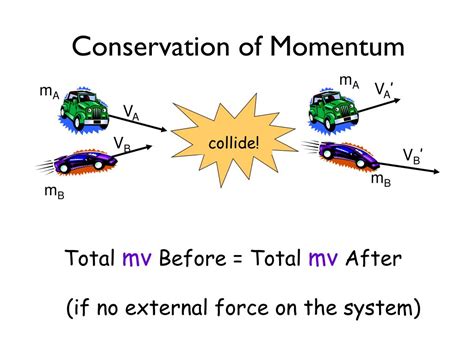
Table of Contents
The Total Momentum of a System is Conserved When…
The principle of conservation of momentum is a cornerstone of classical mechanics, providing a powerful tool for analyzing the motion of objects and systems. Understanding when and why momentum is conserved is crucial for solving a wide range of physics problems, from collisions of billiard balls to the complex interactions of celestial bodies. This article delves deep into the conditions under which the total momentum of a system remains constant, exploring the underlying physics and providing illustrative examples.
Understanding Momentum
Before diving into conservation, let's clearly define momentum. Momentum (p) is a vector quantity, meaning it possesses both magnitude and direction. It's defined as the product of an object's mass (m) and its velocity (v):
p = mv
The units of momentum are typically kilogram-meters per second (kg·m/s). A heavier object moving at the same velocity as a lighter object will have a greater momentum. Similarly, an object moving at a higher velocity will have greater momentum than an object of the same mass moving at a lower velocity.
The Law of Conservation of Momentum
The law of conservation of momentum states that the total momentum of a closed system remains constant if no external forces act on the system. This means that the total momentum before an event (like a collision) is equal to the total momentum after the event. Mathematically, this can be expressed as:
p<sub>initial</sub> = p<sub>final</sub>
Or, more explicitly for a system with multiple objects:
∑p<sub>initial,i</sub> = ∑p<sub>final,i</sub>
where the summation (∑) represents the sum of the momenta of all objects (i) in the system.
This law is a direct consequence of Newton's third law of motion – for every action, there is an equal and opposite reaction. When two objects interact, they exert forces on each other. These forces are equal in magnitude and opposite in direction, resulting in equal and opposite changes in momentum. Therefore, the net change in momentum for the system is zero.
Conditions for Conservation of Momentum
The key condition for the conservation of momentum is the absence of external forces. Let's break this down further:
1. Closed System:
A closed system, also known as an isolated system, is a system that does not exchange matter or energy with its surroundings. This is a crucial requirement. If the system is open, external forces can alter the momentum. For example, consider a rocket launching. The rocket expels gas, exchanging both matter and momentum with the surroundings. Hence, the momentum of the rocket alone is not conserved. However, if we consider the system to be the rocket plus the expelled gas, the total momentum of the combined system is conserved.
2. No Net External Force:
Even in a closed system, if a net external force acts on the system, momentum is not conserved. Consider a ball rolling across a rough surface. Friction acts as an external force, slowing the ball down and thus changing its momentum. The system isn't closed because friction transfers energy into heat.
3. Internal Forces Only:
Internal forces are forces that act within the system. These forces are always paired according to Newton's Third Law. They cannot change the total momentum of the system, only redistribute it among the objects within the system. Examples of internal forces include:
- Gravitational forces between objects within a system (e.g., planets in a solar system).
- Electromagnetic forces between charged particles within a system.
- Contact forces during collisions.
These forces cause changes in individual momenta within the system, but the total momentum remains constant as long as no external forces are involved.
Examples of Conservation of Momentum
Let's explore some practical examples to illustrate the principle:
1. Collision of Billiard Balls:
Consider two billiard balls colliding on a frictionless table (negligible external forces). The total momentum of the two balls before the collision will be equal to the total momentum after the collision. Momentum is transferred from one ball to the other during the collision, but the total remains constant.
2. Rocket Propulsion:
As mentioned earlier, a rocket's propulsion is a prime example where the system needs to be considered carefully to see momentum conservation. The rocket expels hot gas, thereby losing mass. The momentum of the expelled gas is equal and opposite to the momentum gained by the rocket. The total momentum of the rocket plus the expelled gas remains constant.
3. Explosions:
During an explosion, an object at rest breaks apart into multiple pieces. The initial momentum is zero. After the explosion, the total momentum of all the fragments must still sum to zero. Each fragment will have a momentum, and these momenta will add vectorially to zero.
4. Recoil of a Gun:
When a gun is fired, the bullet is propelled forward with a significant momentum. To conserve momentum, the gun recoils backward with an equal and opposite momentum. The larger mass of the gun means its velocity is smaller than that of the bullet, but the momentum is the same in magnitude.
5. Elastic and Inelastic Collisions:
- Elastic Collisions: In an elastic collision, both kinetic energy and momentum are conserved. This is an idealization, as real-world collisions always involve some energy loss due to factors like heat and sound. Examples include collisions between very hard objects like billiard balls (approximately elastic).
- Inelastic Collisions: In an inelastic collision, momentum is conserved, but kinetic energy is not. Some kinetic energy is transformed into other forms of energy, such as heat, sound, or deformation. Examples include car crashes, where significant deformation occurs.
Applications of Conservation of Momentum
The principle of conservation of momentum has broad applications across various fields:
- Nuclear and Particle Physics: Understanding momentum conservation is essential in analyzing nuclear reactions and particle collisions, where high-energy particles interact.
- Astrophysics: Studying the motion of stars, planets, and galaxies involves applying the conservation of momentum to understand gravitational interactions and orbital dynamics.
- Engineering: Designing rockets, automobiles, and other systems relies heavily on understanding the conservation of momentum to predict forces and motions.
- Sports: Analyzing the motion of balls, athletes, and equipment in various sports benefits from the application of this principle.
Beyond Classical Mechanics:
While we've focused on classical mechanics, the principle of conservation of momentum holds true even in relativistic mechanics (at speeds approaching the speed of light) albeit with a modified definition of momentum that accounts for relativistic effects.
Conclusion
The total momentum of a system is conserved when the system is closed and no net external forces act upon it. This fundamental principle is a powerful tool for analyzing a vast array of physical phenomena, from simple collisions to complex interactions in the cosmos. Understanding the conditions for its applicability is crucial for correctly applying this law and making accurate predictions about the behavior of physical systems. By grasping the concepts explained herein, you can confidently analyze and solve numerous problems involving momentum and its conservation. Remember to always carefully define your system and account for all forces involved for accurate results.
Latest Posts
Latest Posts
-
How Is A Voltmeter Connected In A Circuit
Apr 06, 2025
-
45 Minutes Is What Fraction Of An Hour
Apr 06, 2025
-
If The Diagonals Of A Quadrilateral Bisect Each Other
Apr 06, 2025
-
In An Oxidation Reduction Reaction The Substance Oxidized Always
Apr 06, 2025
-
Fungal Cell Walls Consist Primarily Of
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about The Total Momentum Of A System Is Conserved __________. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
