If The Diagonals Of A Quadrilateral Bisect Each Other
News Leon
Apr 06, 2025 · 5 min read
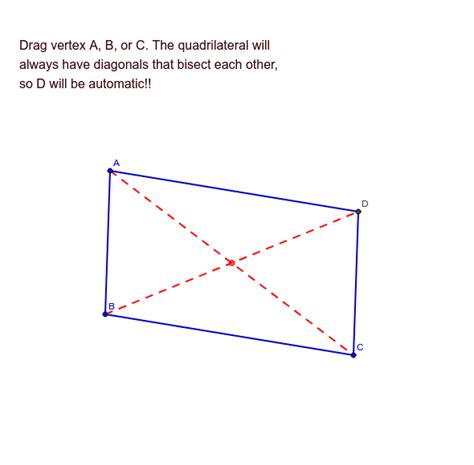
Table of Contents
If the Diagonals of a Quadrilateral Bisect Each Other
The properties of quadrilaterals are a fascinating area of geometry, offering a rich landscape of theorems, proofs, and applications. One particularly insightful property centers around the diagonals of a quadrilateral and their behavior when they bisect each other. This article delves deep into this concept, exploring its implications, proving the fundamental theorem, and examining related geometrical concepts. We'll explore the characteristics of this specific type of quadrilateral and distinguish it from other quadrilateral types.
Understanding Quadrilaterals and Their Diagonals
Before diving into the specifics of bisecting diagonals, let's establish a foundational understanding of quadrilaterals and their diagonals. A quadrilateral is simply a polygon with four sides. Examples include squares, rectangles, rhombuses, parallelograms, trapezoids, and kites – each with its unique set of properties. The diagonals of a quadrilateral are the line segments connecting opposite vertices. These diagonals play a crucial role in determining the properties and classification of the quadrilateral.
Types of Quadrilaterals: A Quick Overview
To fully appreciate the significance of bisecting diagonals, it's beneficial to briefly review the key characteristics of common quadrilaterals:
- Parallelogram: A quadrilateral where opposite sides are parallel and equal in length. Opposite angles are also equal.
- Rectangle: A parallelogram where all angles are right angles (90 degrees).
- Rhombus: A parallelogram where all sides are equal in length.
- Square: A quadrilateral that is both a rectangle and a rhombus – all sides are equal, and all angles are right angles.
- Trapezoid (or Trapezium): A quadrilateral with at least one pair of parallel sides.
- Kite: A quadrilateral with two pairs of adjacent sides that are equal in length.
The Theorem: If the Diagonals Bisect Each Other...
The central theorem we'll explore states: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram. This means that if the point of intersection of the diagonals divides each diagonal into two equal segments, the quadrilateral possesses all the properties of a parallelogram.
Proof of the Theorem
Let's prove this theorem using coordinate geometry. This approach allows for a rigorous and clear demonstration.
1. Setup:
Consider a quadrilateral ABCD, where the diagonals AC and BD intersect at point O. Let's assume that the diagonals bisect each other. This means:
- AO = OC
- BO = OD
2. Coordinate Assignment:
Let's assign coordinates to the vertices:
- A = (x₁, y₁)
- B = (x₂, y₂)
- C = (x₃, y₃)
- D = (x₄, y₄)
Since the diagonals bisect each other, the coordinates of O can be expressed as the midpoint of both AC and BD:
- O = ((x₁ + x₃)/2, (y₁ + y₃)/2) (Midpoint of AC)
- O = ((x₂ + x₄)/2, (y₂ + y₄)/2) (Midpoint of BD)
3. Equating Coordinates:
Since both expressions represent the coordinates of O, we can equate them:
- (x₁ + x₃)/2 = (x₂ + x₄)/2 => x₁ + x₃ = x₂ + x₄
- (y₁ + y₃)/2 = (y₂ + y₄)/2 => y₁ + y₃ = y₂ + y₄
4. Demonstrating Parallelogram Properties:
To prove ABCD is a parallelogram, we need to show that opposite sides are parallel. We can do this by showing that the slopes of opposite sides are equal.
The slope of AB is (y₂ - y₁)/(x₂ - x₁) The slope of CD is (y₄ - y₃)/(x₄ - x₃) The slope of BC is (y₃ - y₂)/(x₃ - x₂) The slope of AD is (y₁ - y₄)/(x₁ - x₄)
From the equations derived in step 3, we can manipulate them to demonstrate that the slopes of AB and CD are equal, and the slopes of BC and AD are equal. This algebraic manipulation is somewhat involved but ultimately proves that opposite sides are parallel. (Detailed algebraic steps omitted for brevity but are readily available in standard geometry textbooks).
5. Conclusion:
Since opposite sides are parallel, ABCD is a parallelogram. Therefore, we have proven the theorem: If the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Converse of the Theorem
The converse of this theorem is also true: If a quadrilateral is a parallelogram, then its diagonals bisect each other. This can be proven using similar geometric arguments, often involving congruent triangles formed by the diagonals.
Implications and Applications
The theorem concerning bisecting diagonals has significant implications in various areas of mathematics and its applications:
- Vector Geometry: This theorem finds application in vector addition and subtraction. The diagonal of a parallelogram can be represented as the vector sum of its adjacent sides.
- Engineering and Physics: The concept of parallel forces and their resultant is directly related to parallelogram properties, hence, to bisecting diagonals.
- Computer Graphics: Parallelograms are fundamental shapes used in computer graphics for creating more complex shapes and transformations. Understanding their diagonal properties is crucial for efficient algorithms.
- Architectural Design: The principles of geometry, including parallelogram properties, are used extensively in architectural design to ensure structural stability and aesthetic balance.
Distinguishing from Other Quadrilaterals
It is crucial to understand that not all quadrilaterals have diagonals that bisect each other. Only parallelograms (and therefore, rectangles, rhombuses, and squares) satisfy this condition. Trapezoids, kites, and other irregular quadrilaterals do not have this property. This distinction helps in classifying and analyzing different quadrilateral shapes.
Further Exploration: Beyond the Basics
This exploration of bisecting diagonals opens doors to more advanced geometric concepts:
- Centroid of a Quadrilateral: The intersection point of the diagonals in a parallelogram is also its centroid, a point of significant importance in various mathematical applications.
- Area of a Parallelogram: The area of a parallelogram can be elegantly calculated using its diagonals and the angle between them.
- Isosceles Trapezoids: While not all trapezoids have bisecting diagonals, isosceles trapezoids exhibit unique properties related to diagonal lengths.
Conclusion
The seemingly simple property of bisecting diagonals within a quadrilateral reveals a profound connection to the properties of parallelograms. The theorem, its proof, and its implications illuminate fundamental geometric principles and have practical applications across diverse fields. Through a deeper understanding of this concept, we gain valuable insights into the rich tapestry of geometric shapes and their relationships. The rigorous exploration of this theorem exemplifies the power of mathematical reasoning and its ability to unlock hidden connections within seemingly disparate geometric concepts. The ability to confidently identify a parallelogram based solely on the behavior of its diagonals is a testament to the elegance and utility of geometric theorems.
Latest Posts
Latest Posts
-
A Number Is Divisible By 2 If
Apr 06, 2025
-
What Is 0 07 Written As A Percent
Apr 06, 2025
-
Select The Atoms That Belong To The Same Element
Apr 06, 2025
-
Is Amoeba A Prokaryote Or Eukaryote
Apr 06, 2025
-
R Is The Midpoint Of Qs
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about If The Diagonals Of A Quadrilateral Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
