How To Determine The Maximum Height Of A Projectile
News Leon
Mar 31, 2025 · 5 min read
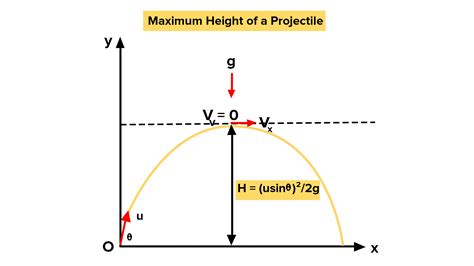
Table of Contents
How to Determine the Maximum Height of a Projectile
Determining the maximum height a projectile reaches is a fundamental concept in physics with applications ranging from sports to aerospace engineering. Understanding the factors that influence this height and the methods used to calculate it is crucial for anyone studying projectile motion. This comprehensive guide will delve into the intricacies of projectile motion, providing you with a thorough understanding of how to determine the maximum height a projectile can achieve.
Understanding Projectile Motion
Projectile motion is the motion of an object thrown or projected into the air, subject only to the acceleration due to gravity. We'll ignore air resistance in our calculations for simplicity, although in real-world scenarios, it significantly impacts the trajectory. The path a projectile follows is a parabola. Key characteristics of projectile motion include:
- Initial Velocity: The speed and direction at which the projectile is launched. This is often broken down into horizontal (Vx) and vertical (Vy) components.
- Angle of Projection: The angle at which the projectile is launched relative to the horizontal.
- Acceleration due to Gravity (g): A constant downward acceleration acting on the projectile (approximately 9.8 m/s² on Earth).
These three factors completely define the projectile's trajectory, including its maximum height.
The Role of Gravity
Gravity is the primary force influencing the vertical motion of a projectile. It constantly pulls the projectile downwards, causing its vertical velocity to decrease until it reaches its highest point, where the vertical velocity becomes zero. After this point, gravity continues to act, causing the projectile to accelerate downwards and fall back to the ground.
Calculating Maximum Height: The Equations
We can use kinematic equations to determine the maximum height (H) a projectile reaches. These equations relate initial velocity, acceleration, time, and displacement. Focusing on the vertical component of the motion, the relevant equation is:
v² = u² + 2as
Where:
- v is the final vertical velocity (0 m/s at the maximum height)
- u is the initial vertical velocity (Vy)
- a is the acceleration due to gravity (-g, negative because it acts downwards)
- s is the vertical displacement (H, the maximum height)
Substituting the values, we get:
0 = Vy² - 2gH
Solving for H, we arrive at the equation for maximum height:
H = Vy² / 2g
This equation shows that the maximum height is directly proportional to the square of the initial vertical velocity and inversely proportional to the acceleration due to gravity. A higher initial vertical velocity leads to a greater maximum height, while a stronger gravitational field leads to a lower maximum height.
Determining Vy: Resolving the Initial Velocity
The initial vertical velocity (Vy) isn't directly given in most problems. Instead, we usually know the initial velocity (V) and the angle of projection (θ). We can use trigonometry to resolve the initial velocity into its horizontal and vertical components:
- Vy = Vsinθ
- Vx = Vcosθ
Substituting Vy into the equation for maximum height, we get:
H = (Vsinθ)² / 2g
This equation allows us to calculate the maximum height knowing only the initial velocity, the angle of projection, and the acceleration due to gravity.
Practical Applications and Examples
The principles of projectile motion and the calculation of maximum height are essential in numerous fields:
Sports:
- Basketball: Determining the optimal launch angle and velocity to achieve maximum height for a successful shot.
- Long Jump: Understanding the trajectory to maximize the horizontal distance covered.
- Golf: Calculating the launch angle and velocity to achieve the desired distance and height.
Military Applications:
- Ballistics: Determining the trajectory and maximum height of projectiles such as artillery shells or rockets.
- Missile Guidance Systems: Precise calculations are critical for accurate targeting.
Engineering:
- Aerospace Engineering: Designing rockets and other projectiles to reach specific altitudes.
- Civil Engineering: Analyzing the trajectory of objects thrown or dropped during construction.
Example 1: A ball is thrown with an initial velocity of 20 m/s at an angle of 30° to the horizontal. Calculate its maximum height.
Given:
- V = 20 m/s
- θ = 30°
- g = 9.8 m/s²
First, find Vy:
Vy = Vsinθ = 20sin(30°) = 10 m/s
Now, calculate H:
H = Vy² / 2g = (10 m/s)² / (2 * 9.8 m/s²) ≈ 5.1 m
Therefore, the maximum height reached by the ball is approximately 5.1 meters.
Example 2: A rocket is launched vertically with an initial velocity of 100 m/s. Ignoring air resistance, what is its maximum height?
In this case, the angle of projection is 90° (straight upwards), so Vy = V.
H = V² / 2g = (100 m/s)² / (2 * 9.8 m/s²) ≈ 510.2 m
The rocket reaches a maximum height of approximately 510.2 meters.
Factors Affecting Maximum Height in Real-World Scenarios
While the equations presented provide a good approximation, several real-world factors can significantly affect the maximum height of a projectile:
-
Air Resistance: Air resistance opposes the motion of the projectile, reducing its velocity and thus its maximum height. This effect is more pronounced for projectiles with larger surface areas or at higher velocities.
-
Wind: Wind can alter the projectile's trajectory, affecting both its horizontal and vertical components. Headwinds reduce the maximum height, while tailwinds increase it.
-
Variations in Gravity: The acceleration due to gravity is not perfectly constant. It varies slightly depending on altitude and location on Earth.
-
Shape and Spin of the Projectile: The shape and spin of a projectile can affect its air resistance and thus its trajectory. A spinning projectile can experience the Magnus effect, causing it to deviate from its ideal parabolic path.
Advanced Considerations and Modeling
For more accurate predictions of projectile motion, especially in scenarios where air resistance is significant, more complex models are necessary. These often involve numerical methods or computational fluid dynamics (CFD) to solve the equations of motion that include air resistance terms. These models often use differential equations to capture the continuous change in velocity and position of the projectile.
Conclusion
Determining the maximum height of a projectile is a crucial calculation in various fields. While the basic kinematic equations provide a good understanding and approximation, remembering the limitations and considering real-world factors leads to a more comprehensive analysis. By understanding the principles of projectile motion and utilizing the appropriate equations, you can accurately predict the maximum height a projectile will reach. As you progress in your studies or applications, incorporating more complex models will allow for even greater accuracy and a deeper understanding of this fascinating area of physics.
Latest Posts
Latest Posts
-
Every Integer Is A Real Number
Apr 01, 2025
-
Count Vowels In A String Python
Apr 01, 2025
-
Which Of The Following Elements Is Most Electronegative
Apr 01, 2025
-
For Which Value Of X Is Abcd A Kite
Apr 01, 2025
-
64 To The Power Of 1 2
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Determine The Maximum Height Of A Projectile . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
