Which Characteristic Is Given By The Angular Momentum Quantum Number
News Leon
Mar 28, 2025 · 6 min read
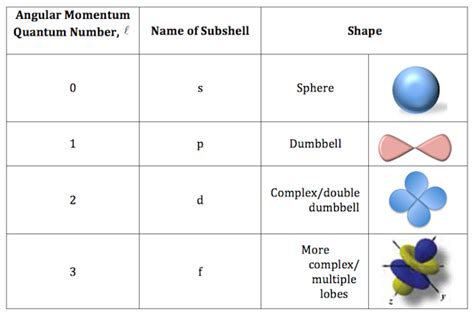
Table of Contents
Which Characteristic is Given by the Angular Momentum Quantum Number?
The angular momentum quantum number, denoted by l, is a crucial component in understanding the behavior of electrons within an atom. It doesn't directly tell us the magnitude of the angular momentum (that requires a more complex calculation involving both l and Planck's constant), but it dictates the shape of the electron's orbital and contributes significantly to its energy level. This article delves deep into the significance of l, exploring its relationship with other quantum numbers, its impact on atomic properties, and its practical applications in chemistry and physics.
Understanding the Angular Momentum Quantum Number (l)
The angular momentum quantum number is an integer value that describes the shape of an electron's atomic orbital. It's intrinsically linked to the principal quantum number (n), which defines the energy level of the electron. l can have any integer value from 0 to n - 1. This means:
- For n = 1, l can only be 0.
- For n = 2, l can be 0 or 1.
- For n = 3, l can be 0, 1, or 2.
- And so on.
Each value of l corresponds to a specific subshell and orbital shape:
- l = 0: This represents the s subshell. S orbitals are spherically symmetric; they have a single lobe centered around the nucleus.
- l = 1: This represents the p subshell. P orbitals are dumbbell-shaped, with two lobes oriented along a specific axis (x, y, or z). There are three p orbitals per subshell.
- l = 2: This represents the d subshell. D orbitals have more complex shapes, including cloverleaf and doughnut-like forms. There are five d orbitals per subshell.
- l = 3: This represents the f subshell. F orbitals have even more intricate shapes. There are seven f orbitals per subshell.
The pattern continues for higher values of l, although these are less commonly encountered in everyday chemistry. The shapes of the orbitals directly influence the electron's probability density distribution around the nucleus – where the electron is most likely to be found.
The Relationship Between l and Other Quantum Numbers
The angular momentum quantum number is not an isolated entity; it interacts intricately with other quantum numbers to completely define an electron's state within an atom. These include:
- Principal Quantum Number (n): As discussed, n determines the energy level and size of the orbital. l is directly dependent on n.
- Magnetic Quantum Number (m<sub>l</sub>): This quantum number describes the orientation of the orbital in space. m<sub>l</sub> can have integer values ranging from –l to +l, including 0. For example, if l = 1 (p subshell), m<sub>l</sub> can be –1, 0, or +1, representing the three p orbitals (p<sub>x</sub>, p<sub>y</sub>, p<sub>z</sub>) oriented along the x, y, and z axes, respectively.
- Spin Quantum Number (m<sub>s</sub>): This describes the intrinsic angular momentum of the electron, often visualized as "spin up" (+1/2) or "spin down" (–1/2). While not directly related to l, it's crucial for understanding electron configuration and the Pauli Exclusion Principle.
The combination of these four quantum numbers (n, l, m<sub>l</sub>, and m<sub>s</sub>) uniquely defines the quantum state of an individual electron within an atom. No two electrons can have the same set of all four quantum numbers, a principle known as the Pauli Exclusion Principle.
Impact of l on Atomic Properties
The angular momentum quantum number profoundly influences several atomic properties:
- Orbital Shape and Size: As mentioned earlier, l dictates the orbital shape. Higher values of l generally result in more complex and larger orbitals, with increased probability density further from the nucleus.
- Energy Levels: While the principal quantum number (n) is the primary determinant of energy, l also contributes, albeit to a lesser extent. For a given n, orbitals with higher l values typically have slightly higher energy. This is known as the penetrating power effect where the s-orbital electrons spend more time closer to the nucleus than p-orbital electrons.
- Bonding and Reactivity: The shape and spatial orientation of orbitals, determined by l, play a vital role in chemical bonding. The overlap of orbitals between atoms forms molecular orbitals, dictating the strength and nature of the bond. The reactivity of an atom is also heavily influenced by the availability of electrons in different subshells.
- Spectroscopic Properties: The energy differences between orbitals with different l values determine the wavelengths of light absorbed or emitted during electronic transitions. This is fundamental to atomic spectroscopy, allowing us to identify elements based on their unique spectral fingerprints.
- Magnetic Properties: The orbital angular momentum associated with l contributes to the overall magnetic moment of an atom. This is crucial in understanding the behavior of atoms in magnetic fields, such as in Nuclear Magnetic Resonance (NMR) spectroscopy.
Applications of the Angular Momentum Quantum Number
The angular momentum quantum number's importance extends beyond theoretical understanding; it has numerous practical applications:
- Chemistry: l is essential in predicting molecular geometry, understanding chemical bonding (sigma and pi bonds), explaining reactivity trends, and interpreting spectroscopic data. It's a cornerstone of valence bond theory and molecular orbital theory, used to construct and understand chemical bonds.
- Physics: In atomic and nuclear physics, l is fundamental for understanding atomic structure, spectral lines, and the interactions of atoms with electromagnetic fields. It contributes to our understanding of how electrons occupy different shells and subshells within atoms.
- Materials Science: The concept of orbitals and their shapes (determined by l) helps us understand the electronic structure of materials, which dictates their physical and chemical properties. This is critical for designing novel materials with specific functionalities.
- Nanotechnology: At the nanoscale, understanding the behavior of electrons in atomic orbitals becomes even more vital. l plays a crucial role in predicting the properties of nanoscale materials and designing nanoscale devices.
Advanced Concepts and Further Considerations
While the basic understanding of l involves its integer values and their corresponding orbital shapes, deeper exploration reveals more nuanced aspects:
- Orbital Angular Momentum Vector: l is related to the magnitude of the orbital angular momentum vector. The magnitude of this vector is given by √(l(l+1))ħ, where ħ is the reduced Planck's constant.
- Spin-Orbit Coupling: The interaction between the electron's spin angular momentum and its orbital angular momentum (influenced by l) leads to spin-orbit coupling, causing slight energy shifts in the orbitals.
- Relativistic Effects: At higher atomic numbers, relativistic effects become significant, altering the energy levels and orbital shapes influenced by l.
Conclusion
The angular momentum quantum number (l) is a critical parameter in atomic physics and chemistry. It dictates the shape of atomic orbitals, influences the energy levels of electrons, and plays a vital role in numerous atomic and molecular properties. Understanding its relationship with other quantum numbers and its impact on various phenomena is paramount for a comprehensive understanding of matter's fundamental behavior and has significant implications across various scientific disciplines. Its application extends from predicting chemical reactivity to designing cutting-edge materials, highlighting its enduring importance in scientific advancement. The seemingly simple integer value of l holds immense power in unraveling the complexities of the atom and the molecules it forms.
Latest Posts
Latest Posts
-
An Alloy Consists Of Nickel Zinc And Copper
Mar 31, 2025
-
What Is The Potential Difference Across The 40 O Resistor
Mar 31, 2025
-
Look At The Figure Find The Length Of
Mar 31, 2025
-
What Is The Bond Order Of No
Mar 31, 2025
-
Two Small Metal Spheres Are Connected By A Wire
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Which Characteristic Is Given By The Angular Momentum Quantum Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
