What Is The Potential Difference Across The 40 Ω Resistor
News Leon
Mar 31, 2025 · 6 min read
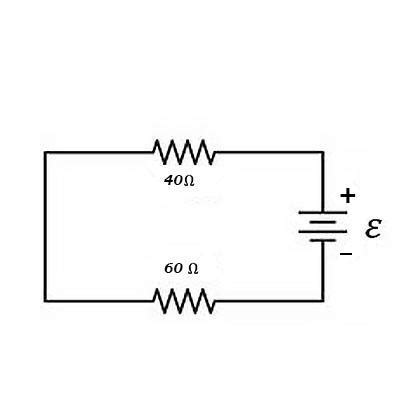
Table of Contents
What is the Potential Difference Across the 40Ω Resistor? A Deep Dive into Circuit Analysis
Understanding potential difference, or voltage, across a resistor is fundamental to circuit analysis. This article will delve deep into calculating the potential difference across a 40Ω resistor, exploring various circuit configurations and methodologies. We'll cover simple series and parallel circuits, then move onto more complex scenarios involving multiple resistors and voltage sources. By the end, you'll possess a solid understanding of the principles and techniques involved.
Understanding Potential Difference (Voltage)
Before diving into calculations, let's solidify our understanding of potential difference. Potential difference, measured in volts (V), represents the work done per unit charge in moving a charge between two points in a circuit. It's the electrical pressure that drives the flow of current. In simpler terms, it's the difference in electrical potential energy between two points. A higher potential difference indicates a greater driving force for current.
Ohm's Law: The Foundation of Circuit Analysis
Ohm's Law forms the cornerstone of our calculations. It states that the current (I) flowing through a resistor is directly proportional to the potential difference (V) across it and inversely proportional to its resistance (R). Mathematically, it's expressed as:
V = I * R
Where:
- V is the potential difference (voltage) in volts (V)
- I is the current in amperes (A)
- R is the resistance in ohms (Ω)
This simple yet powerful equation allows us to calculate any one of these three parameters if we know the other two.
Calculating Potential Difference in Simple Circuits
Let's begin with simple circuit configurations to illustrate the application of Ohm's Law.
Series Circuit
In a series circuit, components are connected end-to-end, forming a single path for current flow. The current is the same throughout the entire circuit. To find the potential difference across the 40Ω resistor in a series circuit, we need the total current and the resistor's value.
Example: Imagine a series circuit with a 12V battery and two resistors: a 40Ω resistor and a 60Ω resistor.
-
Total Resistance: In a series circuit, the total resistance (R<sub>T</sub>) is the sum of individual resistances: R<sub>T</sub> = R<sub>1</sub> + R<sub>2</sub> = 40Ω + 60Ω = 100Ω
-
Total Current: Using Ohm's Law, we calculate the total current (I) in the circuit: I = V / R<sub>T</sub> = 12V / 100Ω = 0.12A
-
Potential Difference Across the 40Ω Resistor: Since the current is the same throughout a series circuit, the potential difference (V<sub>40Ω</sub>) across the 40Ω resistor is: V<sub>40Ω</sub> = I * R<sub>40Ω</sub> = 0.12A * 40Ω = 4.8V
Parallel Circuit
In a parallel circuit, components are connected across each other, providing multiple paths for current flow. The voltage across each branch is the same, but the current is divided among the branches.
Example: Consider a parallel circuit with a 12V battery and two resistors: a 40Ω resistor and a 60Ω resistor.
-
Voltage Across the 40Ω Resistor: In a parallel circuit, the voltage across each resistor is equal to the source voltage. Therefore, the potential difference across the 40Ω resistor (V<sub>40Ω</sub>) is directly 12V.
-
Current Through the 40Ω Resistor: We can then calculate the current (I<sub>40Ω</sub>) through the 40Ω resistor using Ohm's Law: I<sub>40Ω</sub> = V<sub>40Ω</sub> / R<sub>40Ω</sub> = 12V / 40Ω = 0.3A
More Complex Circuits: Kirchhoff's Laws
For circuits with multiple voltage sources and complex arrangements of resistors, we need to employ Kirchhoff's Laws:
-
Kirchhoff's Current Law (KCL): The sum of currents entering a junction (node) equals the sum of currents leaving that junction. This law reflects the conservation of charge.
-
Kirchhoff's Voltage Law (KVL): The sum of potential differences (voltages) around any closed loop in a circuit is zero. This law reflects the conservation of energy.
These laws, combined with Ohm's Law, allow us to systematically solve for unknown voltages and currents in even the most intricate circuits. Solving these circuits often involves setting up and solving systems of simultaneous equations. Techniques like nodal analysis or mesh analysis can simplify the process.
Influence of Internal Resistance
Real-world voltage sources, such as batteries, possess internal resistance. This internal resistance reduces the terminal voltage (the voltage available at the terminals of the battery) when current flows. To accurately calculate the potential difference across the 40Ω resistor, we must consider the internal resistance of the voltage source.
Example: A 12V battery with an internal resistance of 2Ω is connected to a 40Ω resistor.
-
Total Resistance: The internal resistance is in series with the 40Ω resistor. Therefore, the total resistance is: R<sub>T</sub> = R<sub>internal</sub> + R<sub>40Ω</sub> = 2Ω + 40Ω = 42Ω
-
Total Current: The current flowing through the circuit is: I = V / R<sub>T</sub> = 12V / 42Ω ≈ 0.286A
-
Potential Difference Across the 40Ω Resistor: The potential difference across the 40Ω resistor is: V<sub>40Ω</sub> = I * R<sub>40Ω</sub> = 0.286A * 40Ω ≈ 11.44V Notice that the potential difference across the 40Ω resistor is slightly less than the battery's emf due to the voltage drop across the internal resistance.
Impact of Non-Linear Components
The examples above focus on linear resistors where Ohm's Law applies directly. However, real-world circuits often include non-linear components like diodes or transistors, where the relationship between voltage and current is not linear. Calculating the potential difference across the 40Ω resistor in such circuits requires more advanced techniques, potentially involving iterative methods or specialized software.
Practical Applications and Importance
Accurately determining the potential difference across a resistor has numerous practical applications in various fields:
- Electronics: Design and troubleshooting of electronic circuits.
- Power Systems: Analyzing power distribution networks and load calculations.
- Telecommunications: Signal processing and transmission.
- Instrumentation: Designing and calibrating measuring instruments.
Understanding these calculations is crucial for engineers, technicians, and anyone involved in designing, building, or maintaining electrical systems.
Conclusion
Calculating the potential difference across a 40Ω resistor, or any resistor for that matter, is a fundamental skill in circuit analysis. The approach depends on the complexity of the circuit. Simple series and parallel circuits can be solved directly using Ohm's Law. More complex circuits require the application of Kirchhoff's Laws, and potentially more advanced techniques for non-linear components. Remember that the internal resistance of voltage sources also impacts the actual voltage drop across the resistor. Mastering these concepts is key to understanding and working effectively with electrical and electronic systems. Further exploration into advanced circuit analysis techniques, such as nodal and mesh analysis, will enhance your ability to tackle even more intricate circuits. Remember to always consider the context of your circuit and choose the appropriate methods for accurate analysis.
Latest Posts
Latest Posts
-
A Short Term Unsecured Promissory Note Issued By A Company Is
Apr 01, 2025
-
Adjacent Angles Whose Sum In 180 Degrees
Apr 01, 2025
-
Lewis Dot Structure For Magnesium Chloride
Apr 01, 2025
-
A Group Of Related Records Is Called A Table
Apr 01, 2025
-
Provides Long Term Energy Storage For Animals
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Is The Potential Difference Across The 40 Ω Resistor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
