Adjacent Angles Whose Sum In 180 Degrees
News Leon
Apr 01, 2025 · 6 min read
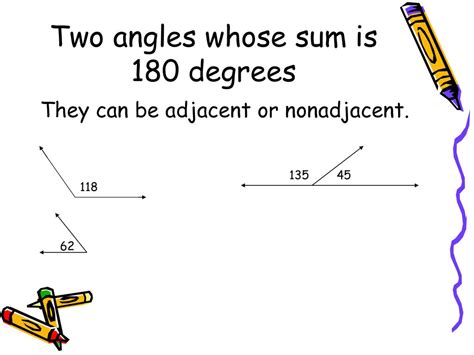
Table of Contents
Adjacent Angles Whose Sum is 180 Degrees: A Deep Dive into Supplementary Angles
Understanding angles is fundamental to geometry and numerous applications in various fields. This comprehensive guide delves into the fascinating world of adjacent angles, specifically focusing on those whose sum equals 180 degrees – a concept crucial for solving geometric problems and understanding spatial relationships. We'll explore the definition, properties, examples, and real-world applications of these angles, often referred to as supplementary angles.
What are Adjacent Angles?
Before diving into supplementary angles, let's solidify our understanding of adjacent angles. Adjacent angles are two angles that share a common vertex (the point where the two rays meet) and a common side, but they do not overlap. Think of them as angles that are "next to" each other. Crucially, they must share a common side and vertex to qualify as adjacent.
Identifying Adjacent Angles
Identifying adjacent angles is straightforward. Look for these key characteristics:
- Common Vertex: Both angles share the same starting point.
- Common Side: One side of one angle is also a side of the other angle.
- No Overlap: The angles do not share any interior points.
Imagine two angles, ∠AOB and ∠BOC. If they share the common vertex O and the common side OB, and they don't overlap, then ∠AOB and ∠BOC are adjacent angles.
Supplementary Angles: The 180-Degree Connection
Now, let's focus on the specific type of adjacent angles that are the subject of this article: supplementary angles. Supplementary angles are two adjacent angles whose measures add up to 180 degrees. This is a critical relationship in geometry, allowing us to solve for unknown angles and establish spatial relationships. The sum of their measures must precisely equal 180 degrees. If the sum is more or less, they are not supplementary.
Key Properties of Supplementary Angles
- Sum is 180°: This is the defining characteristic. The sum of the measures of two supplementary angles always equals 180 degrees.
- Adjacent (Usually): While it's possible for non-adjacent angles to be supplementary, the most common scenario involves adjacent angles.
- Linear Pair: A special case of supplementary angles is a linear pair. A linear pair consists of two adjacent angles formed when two lines intersect. Because they form a straight line, their sum is always 180 degrees. All linear pairs are supplementary, but not all supplementary angles are linear pairs.
Examples of Supplementary Angles
Let's illustrate supplementary angles with several examples:
Example 1: Adjacent Supplementary Angles
Imagine a straight line. Draw a ray from a point on that line, creating two angles. These two angles are adjacent and supplementary. If one angle measures 110 degrees, the other automatically measures 70 degrees (180° - 110° = 70°).
Example 2: Non-Adjacent Supplementary Angles
Consider a quadrilateral (a four-sided shape). Imagine two angles that are not adjacent to each other. If the sum of their measures is 180 degrees, they are still supplementary, even though they don't share a common side.
Example 3: Linear Pair
Draw two intersecting lines. Notice that four angles are formed. Any two angles that are adjacent and form a straight line form a linear pair and are supplementary.
Solving Problems with Supplementary Angles
Supplementary angles are invaluable in solving geometric problems. Knowing that two angles are supplementary allows you to find the measure of one angle if you know the measure of the other. Many problems in geometry rely on this principle.
Problem Solving Techniques
Here's a step-by-step approach to solve problems involving supplementary angles:
- Identify the Supplementary Angles: Determine which angles are supplementary based on the problem's description and diagram.
- Set up an Equation: Let 'x' represent the measure of one angle. Express the measure of the other angle in terms of 'x' using the relationship that their sum is 180 degrees.
- Solve for x: Solve the equation for 'x' to find the measure of one angle.
- Find the Other Angle: Substitute the value of 'x' back into the equation to find the measure of the other angle.
- Check your Answer: Verify that the sum of the two angles equals 180 degrees.
Real-World Applications of Supplementary Angles
The concept of supplementary angles isn't confined to geometry textbooks; it has practical applications in various fields:
-
Architecture and Construction: Architects and engineers use supplementary angles to ensure that structures are stable and properly aligned. For instance, when designing roof structures or supporting beams, the angles must be carefully calculated to ensure structural integrity. Understanding supplementary angles ensures the correct angle calculations for precise constructions.
-
Navigation and Surveying: Supplementary angles are crucial in navigation and surveying. Determining bearings and directions often relies on calculating supplementary angles to accurately map terrain and chart courses.
-
Computer Graphics and Game Development: In computer graphics and game development, supplementary angles are used extensively in creating realistic 3D models and animations. Precise angle calculations are essential for rendering objects accurately and for smooth and realistic movement.
-
Engineering and Robotics: In robotics and engineering, understanding supplementary angles is critical for designing robotic arms and other mechanical systems. Accurate calculations of angles allow for precise movement and control.
-
Art and Design: The principles of supplementary angles are often employed in art and design, particularly in creating symmetrical and balanced compositions. The interplay of angles contributes to visual harmony and aesthetic appeal.
Beyond the Basics: Exploring More Complex Scenarios
While the fundamental concept of supplementary angles is relatively straightforward, its applications can become quite complex in advanced geometric problems. Here are some advanced scenarios where understanding supplementary angles is crucial:
-
Polygons: The interior angles of polygons (shapes with three or more sides) have specific relationships that often involve supplementary angles. For example, in a triangle, the sum of the interior angles is 180 degrees, showcasing a direct relationship with supplementary angles.
-
Trigonometry: Supplementary angles play a vital role in trigonometry. Understanding their properties allows for simplification of trigonometric calculations and identities. The relationships between sine, cosine, and tangent of supplementary angles are fundamental to trigonometric problem-solving.
-
Three-Dimensional Geometry: In three-dimensional geometry, supplementary angles are essential for calculating angles between planes and lines in space, essential for spatial reasoning and calculations within three-dimensional objects.
Conclusion: The Enduring Importance of Supplementary Angles
Supplementary angles, while seemingly a simple geometric concept, form the foundation for understanding and solving a wide range of geometric problems. Their applications extend far beyond the classroom, playing a crucial role in various fields requiring precise calculations and spatial reasoning. Mastering the concept of supplementary angles provides a solid foundation for further exploration in geometry and related fields, allowing for accurate calculations and a deeper understanding of spatial relationships. From designing buildings to programming robots, the 180-degree connection between these adjacent angles unlocks a world of possibilities. Understanding and applying the principles of supplementary angles is key for success in various disciplines and in solving complex geometric problems efficiently.
Latest Posts
Latest Posts
-
What Phase Does The Cytoplasm Divide
Apr 02, 2025
-
A Clique Is A Group Of
Apr 02, 2025
-
Determine The Quantity Of Molecules In 2 00 Moles Of P4
Apr 02, 2025
-
Which Of The Following Compounds Have The Same Empirical Formula
Apr 02, 2025
-
An Instrument Used To Measure Atmospheric Pressure Is Called A
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Adjacent Angles Whose Sum In 180 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
