Look At The Figure. Find The Length Of .
News Leon
Mar 31, 2025 · 5 min read
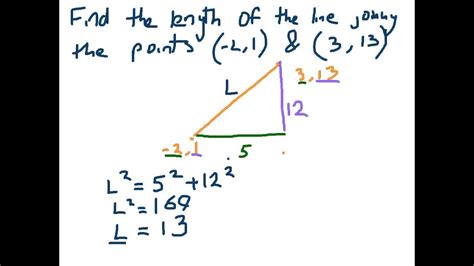
Table of Contents
Look at the Figure: Finding the Length of Unknown Sides
This article delves into the fascinating world of geometry, specifically focusing on the methods used to determine the lengths of unknown sides in various geometric figures. We'll explore different approaches, from basic Pythagorean theorem applications to more advanced trigonometric functions, illustrating each method with practical examples and clear explanations. Understanding these techniques is crucial for success in mathematics, engineering, architecture, and many other fields.
Understanding the Fundamentals: Basic Geometric Shapes
Before we dive into complex calculations, let's review the fundamental shapes and their properties. This foundational knowledge will be crucial for correctly applying the appropriate methods to solve problems involving unknown side lengths.
1. Triangles: The Building Blocks of Geometry
Triangles are arguably the most fundamental geometric shapes. They are categorized based on their sides (equilateral, isosceles, scalene) and angles (acute, right, obtuse). The Pythagorean theorem, applicable only to right-angled triangles, states that the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides (legs). Mathematically, this is expressed as:
a² + b² = c²
Where 'a' and 'b' are the lengths of the legs, and 'c' is the length of the hypotenuse.
2. Rectangles and Squares: Sides and Diagonals
Rectangles are four-sided polygons with four right angles. Squares are special cases of rectangles where all four sides are equal in length. In both rectangles and squares, the lengths of opposite sides are equal. To find the length of the diagonal of a rectangle or square, we again utilize the Pythagorean theorem. Consider a rectangle with sides 'a' and 'b'; the length of the diagonal 'd' is calculated as:
d² = a² + b²
This formula is directly derived from the Pythagorean theorem by considering the diagonal as the hypotenuse of a right-angled triangle formed by two adjacent sides.
3. Circles: Radius, Diameter, and Circumference
Circles are defined by their radius (distance from the center to any point on the circumference) and diameter (twice the radius). The circumference (distance around the circle) is related to the radius (r) or diameter (d) through the following formulas:
- Circumference = 2πr
- Circumference = πd
Where π (pi) is approximately 3.14159.
Advanced Techniques: Trigonometry and Similar Triangles
While the Pythagorean theorem is incredibly useful, it's limited to right-angled triangles. For other triangles, we need to employ trigonometric functions (sine, cosine, tangent) or the concept of similar triangles.
1. Trigonometry: Sine, Cosine, and Tangent
Trigonometric functions relate the angles of a right-angled triangle to the ratios of its sides. For a right-angled triangle with hypotenuse 'c', opposite side 'a', and adjacent side 'b' to angle θ, we have:
- sin θ = a/c
- cos θ = b/c
- tan θ = a/b
These functions allow us to calculate the lengths of unknown sides if we know one side and one angle (besides the right angle).
2. Similar Triangles: Proportional Sides
Similar triangles have the same shape but different sizes. Their corresponding angles are equal, and their corresponding sides are proportional. This means that the ratio of corresponding sides is constant. If we know the lengths of some sides in one triangle and the corresponding sides in a similar triangle, we can use proportions to find the lengths of the unknown sides.
Solving Problems: Step-by-Step Examples
Let's tackle some example problems to solidify our understanding. Remember to always carefully draw a diagram to visualize the problem.
Example 1: Right-Angled Triangle
A right-angled triangle has legs of length 3 cm and 4 cm. Find the length of the hypotenuse.
Solution:
Using the Pythagorean theorem:
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
25 = c²
c = √25 = 5 cm
Therefore, the length of the hypotenuse is 5 cm.
Example 2: Finding a Side Using Trigonometry
A right-angled triangle has a hypotenuse of 10 cm and one angle of 30 degrees. Find the length of the side opposite the 30-degree angle.
Solution:
We use the sine function:
sin θ = opposite/hypotenuse
sin 30° = opposite/10 cm
opposite = 10 cm * sin 30°
Since sin 30° = 0.5,
opposite = 10 cm * 0.5 = 5 cm
The length of the opposite side is 5 cm.
Example 3: Similar Triangles
Two triangles are similar. The first triangle has sides of length 6 cm, 8 cm, and 10 cm. The shortest side of the second triangle is 3 cm. Find the lengths of the other two sides of the second triangle.
Solution:
The ratio of corresponding sides is:
3 cm / 6 cm = 0.5
Therefore, the other sides of the second triangle are:
8 cm * 0.5 = 4 cm
10 cm * 0.5 = 5 cm
The lengths of the other two sides are 4 cm and 5 cm.
Advanced Applications and Further Exploration
The techniques described above form the basis for solving a vast range of geometric problems. Beyond the basic shapes and methods discussed, there are many advanced applications involving more complex figures and three-dimensional geometry. These include:
- Three-Dimensional Geometry: Extending the principles of Pythagorean theorem and trigonometry to three-dimensional shapes like cubes, spheres, and pyramids.
- Vector Geometry: Using vector operations to calculate distances and angles in more complex geometric settings.
- Calculus: Applying calculus to solve problems involving curves and changing dimensions.
Conclusion: Mastering Geometric Calculations
Mastering the art of finding unknown side lengths in geometric figures is a cornerstone of mathematical and scientific understanding. From basic Pythagorean theorem applications to advanced trigonometric calculations and the use of similar triangles, the techniques outlined in this article provide a comprehensive foundation for tackling a wide variety of problems. By understanding these concepts and practicing regularly, you'll build confidence and proficiency in solving geometric problems, opening doors to further exploration in mathematics and related fields. Remember, practice is key! The more problems you solve, the more comfortable and adept you'll become. So, grab your pencil, paper, and a protractor, and start exploring the fascinating world of geometry!
Latest Posts
Latest Posts
-
Which Of The Following Temperatures Is The Coldest
Apr 01, 2025
-
A Short Term Unsecured Promissory Note Issued By A Company Is
Apr 01, 2025
-
Adjacent Angles Whose Sum In 180 Degrees
Apr 01, 2025
-
Lewis Dot Structure For Magnesium Chloride
Apr 01, 2025
-
A Group Of Related Records Is Called A Table
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Look At The Figure. Find The Length Of . . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
