What Physical Quantity Does The Slope Represent
News Leon
Mar 31, 2025 · 7 min read
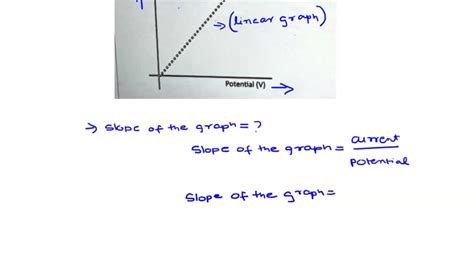
Table of Contents
What Physical Quantity Does the Slope Represent? A Comprehensive Guide
The slope of a graph, a seemingly simple concept, holds immense significance in various fields of science and engineering. Understanding what physical quantity a slope represents is crucial for interpreting data, making predictions, and building a strong foundational understanding of numerous scientific principles. This comprehensive guide will delve into the meaning of slope in different contexts, exploring its physical interpretation and applications across diverse disciplines.
Understanding the Basics: Slope as a Ratio
Before we explore the physical interpretations, let's solidify our understanding of slope in its most basic form. Mathematically, the slope of a line is defined as the ratio of the vertical change (rise) to the horizontal change (run) between any two distinct points on the line. This can be expressed as:
Slope (m) = (y₂ - y₁) / (x₂ - x₁)
where (x₁, y₁) and (x₂, y₂) are the coordinates of two points on the line. A positive slope indicates an upward trend, a negative slope a downward trend, and a slope of zero represents a horizontal line. An undefined slope corresponds to a vertical line.
This simple formula provides the groundwork for interpreting the slope's physical meaning in various applications. The key lies in understanding the physical quantities represented by the 'y' and 'x' axes.
Slope in Different Contexts: A Diverse Landscape of Interpretations
The physical quantity represented by the slope varies dramatically depending on the context of the graph. Let's explore some key examples:
1. Velocity-Time Graphs: Acceleration
In a velocity-time graph, the vertical axis (y-axis) represents velocity (often in meters per second, m/s), and the horizontal axis (x-axis) represents time (often in seconds, s). In this case, the slope represents acceleration.
Slope = (Change in Velocity) / (Change in Time) = Acceleration
This directly relates to Newton's second law of motion (F = ma), where acceleration is the rate of change of velocity. A positive slope indicates positive acceleration (speeding up), a negative slope indicates negative acceleration (slowing down or deceleration), and a slope of zero implies constant velocity. The units of acceleration are typically meters per second squared (m/s²).
2. Position-Time Graphs: Velocity
On a position-time graph, the y-axis represents position (often in meters, m), and the x-axis represents time (s). Here, the slope represents velocity.
Slope = (Change in Position) / (Change in Time) = Velocity
This is a direct representation of how quickly the object is changing its position. A steeper slope means a higher velocity, while a shallower slope indicates a lower velocity. The units of velocity are meters per second (m/s).
3. Force-Extension Graphs: Spring Constant (Hooke's Law)
In the context of Hooke's Law, which describes the elastic behavior of springs, a force-extension graph plots force (often in Newtons, N) on the y-axis and extension (often in meters, m) on the x-axis. The slope of this graph represents the spring constant (k).
Slope = (Change in Force) / (Change in Extension) = Spring Constant (k)
Hooke's Law states that F = kx, where F is the force, k is the spring constant, and x is the extension. The spring constant is a measure of the stiffness of the spring; a steeper slope implies a stiffer spring (higher k). The units of the spring constant are Newtons per meter (N/m).
4. Voltage-Current Graphs: Resistance (Ohm's Law)
Ohm's Law describes the relationship between voltage, current, and resistance in an electrical circuit. A voltage-current graph plots voltage (often in volts, V) on the y-axis and current (often in amperes, A) on the x-axis. The slope of this graph represents the resistance (R).
Slope = (Change in Voltage) / (Change in Current) = Resistance (R)
Ohm's Law states that V = IR, where V is voltage, I is current, and R is resistance. A steeper slope signifies a higher resistance, meaning more voltage is required to produce the same current. The units of resistance are ohms (Ω).
5. Pressure-Volume Graphs: Understanding Gases
In the study of gases, particularly in isothermal processes (constant temperature), a pressure-volume graph is often used. Pressure (often in Pascals, Pa) is plotted on the y-axis and volume (often in cubic meters, m³) on the x-axis. For an isothermal process, the slope is related to the negative of the number of moles of gas multiplied by the gas constant and temperature.
This relationship is derived from the ideal gas law (PV = nRT). The slope's significance lies in providing information about the gas's state and behavior under constant temperature conditions.
6. Concentration-Time Graphs: Reaction Rate
In chemical kinetics, concentration-time graphs are used to study the rate of chemical reactions. Concentration (often in moles per liter, mol/L or M) is plotted on the y-axis, and time (s) on the x-axis. The initial slope of the graph, specifically the negative of the initial slope for reactant concentration, represents the initial rate of reaction.
This initial rate provides valuable insights into the reaction's speed and mechanism. Note that for more complex reactions, the rate may not be constant, and therefore the slope will change over time.
7. Graphs in Economics: Marginal Concepts
In economics, various graphs deal with marginal concepts. For example, a graph of total cost versus quantity produced has a slope representing the marginal cost, which is the cost of producing one more unit of output. Similarly, a graph of total revenue versus quantity sold has a slope representing the marginal revenue, the revenue generated by selling one more unit. These marginal concepts are crucial in decision-making and optimization problems in economics.
8. Gradients in Geography: Steepness of Terrain
In geography, the slope of a line on a topographic map represents the gradient or steepness of the terrain. The steeper the slope, the more inclined the land is. This is essential for understanding landforms, erosion, and other geographical processes. The slope is often expressed as a percentage or angle.
Beyond Simple Linear Relationships: Curves and Tangents
The concept of slope extends beyond simple linear relationships. For curves, the slope at any specific point is given by the tangent to the curve at that point. The slope of the tangent represents the instantaneous rate of change at that particular point. Calculating the slope of a curve often involves calculus, using derivatives to find the instantaneous rate of change. This is crucial in various fields, including physics (e.g., instantaneous velocity), economics (e.g., marginal cost at a specific production level), and many more.
Practical Applications and Importance
Understanding the physical quantity represented by the slope is not merely an academic exercise; it has profound practical applications across various fields:
- Engineering: Slope is crucial for designing structures, calculating stresses and strains, and understanding the behavior of materials.
- Physics: The concept of slope is fundamental in kinematics, dynamics, thermodynamics, and electromagnetism.
- Chemistry: Analyzing reaction rates, equilibrium constants, and other chemical properties relies heavily on interpreting slopes from various graphs.
- Biology: Studying growth rates, population dynamics, and enzyme kinetics often involve analyzing slopes from experimental data.
- Economics: Analyzing marginal costs, marginal revenues, and other economic concepts heavily rely on slope interpretation.
- Data Science and Machine Learning: Linear regression, a fundamental machine learning technique, relies on finding the best-fitting line (and its slope) to predict outcomes based on data.
Conclusion: A Powerful Tool for Understanding Change
The slope of a graph is a powerful tool for understanding and quantifying the rate of change between two variables. Its physical interpretation varies significantly depending on the context, but its fundamental meaning remains consistent: it represents the ratio of the change in the vertical axis to the change in the horizontal axis. Mastering the interpretation of slope is essential for anyone working in a quantitative field, providing a fundamental understanding of how various physical quantities relate and change over time or with respect to other variables. Whether it's acceleration, velocity, spring constant, or resistance, understanding the physical meaning of the slope allows for deeper insights and more accurate predictions.
Latest Posts
Latest Posts
-
A Short Term Unsecured Promissory Note Issued By A Company Is
Apr 01, 2025
-
Adjacent Angles Whose Sum In 180 Degrees
Apr 01, 2025
-
Lewis Dot Structure For Magnesium Chloride
Apr 01, 2025
-
A Group Of Related Records Is Called A Table
Apr 01, 2025
-
Provides Long Term Energy Storage For Animals
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Physical Quantity Does The Slope Represent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
