What Percent Of 12.5 Is 39
News Leon
Mar 28, 2025 · 5 min read
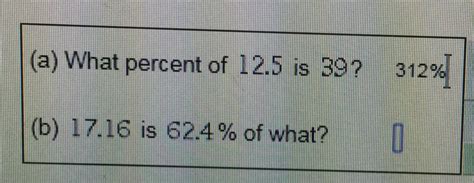
Table of Contents
What Percent of 12.5 is 39? A Deep Dive into Percentage Calculations
This seemingly simple question, "What percent of 12.5 is 39?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and the underlying mathematical principles. While a quick calculation can provide the answer, understanding the how and why behind the process is crucial for anyone navigating the numerical world. This article will not only provide the solution but also delve into the methodology, explore different approaches, and showcase practical applications of percentage calculations.
Understanding Percentages: The Foundation
Percentages are a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" (from the Latin per centum). Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Understanding this fundamental concept is key to tackling percentage problems effectively.
Method 1: The Direct Approach – Using Proportions
The most straightforward way to solve "What percent of 12.5 is 39?" involves setting up a proportion. A proportion is an equation stating that two ratios are equal. In this case, we can set up the following proportion:
x/100 = 39/12.5
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
12.5x = 3900
Then, divide both sides by 12.5:
x = 3900 / 12.5
x = 312
Therefore, 39 is 312% of 12.5.
Method 2: Using Decimal Conversion
Another approach involves converting the percentage to a decimal. We can rewrite the problem as:
x * 12.5 = 39
To solve for 'x', we divide both sides by 12.5:
x = 39 / 12.5
x = 3.12
Since 'x' represents the decimal equivalent of the percentage, we convert it back to a percentage by multiplying by 100:
x = 3.12 * 100 = 312%
This confirms our previous result: 39 is 312% of 12.5.
Method 3: Breaking it Down – Step-by-Step Calculation
For those who prefer a more detailed, step-by-step approach, we can break down the calculation:
-
Find the ratio: Determine the ratio of 39 to 12.5: 39 / 12.5 = 3.12
-
Convert to percentage: Multiply the ratio by 100 to express it as a percentage: 3.12 * 100 = 312%
This method highlights the core principle of percentages: finding the ratio of one number to another and then scaling it to a base of 100.
Understanding the Result: Percentages Greater Than 100%
It's important to note that percentages can exceed 100%. This simply means that the "part" (39 in this case) is larger than the "whole" (12.5). This situation often arises in contexts involving growth, increases, or comparisons where the final value surpasses the initial value. For instance, if a company's revenue increased from 12.5 million to 39 million, the increase would be 312% of the original revenue.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in various aspects of daily life and professional fields:
-
Finance: Calculating interest rates, loan repayments, profit margins, tax rates, discounts, and investment returns all rely heavily on percentage calculations.
-
Retail: Determining sale prices, discounts, and markups are essential aspects of retail operations. Understanding percentages allows businesses to optimize pricing strategies and maximize profits.
-
Science: Many scientific measurements and analyses involve percentages, such as calculating concentrations, error margins, and statistical probabilities.
-
Data Analysis: Percentages are used to represent data proportions, trends, and comparisons in various fields, including business analytics, market research, and social sciences.
-
Everyday Life: Calculating tips, splitting bills, understanding nutritional information on food labels, and tracking personal finances all involve percentage calculations.
Beyond the Basics: Advanced Percentage Problems
While the problem "What percent of 12.5 is 39?" provides a foundational understanding of percentage calculations, more complex scenarios often arise:
-
Percentage increase/decrease: Calculating the percentage change between two values requires subtracting the initial value from the final value, dividing the result by the initial value, and then multiplying by 100.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest, leading to exponential growth over time. Understanding compound interest is critical for long-term financial planning.
-
Percentage points: It's important to differentiate between percentage points and percentage changes. A change of 10 percentage points is different from a 10% change.
Mastering Percentages: Tips and Tricks
To master percentage calculations, consider these tips:
-
Practice regularly: Consistent practice is key to developing fluency and understanding.
-
Use different methods: Experiment with various approaches to solving percentage problems to find the method that suits your understanding best.
-
Break down complex problems: Simplify complex problems into smaller, manageable steps.
-
Utilize online resources: Numerous online calculators, tutorials, and practice problems are available to aid your learning.
-
Understand the context: Always consider the context of the problem to ensure you're applying the correct method and interpreting the results correctly.
Conclusion: More Than Just Numbers
The seemingly simple question, "What percent of 12.5 is 39?", serves as a springboard for understanding the fundamental principles of percentage calculations and their broad applicability. Mastering percentage calculations equips you with a crucial skill set for navigating various aspects of life, from personal finance to professional endeavors. By understanding the underlying concepts, utilizing diverse problem-solving methods, and practicing regularly, you can confidently tackle any percentage-related challenge that comes your way. The ability to work with percentages effectively isn't just about numbers; it's about developing a crucial skill for informed decision-making in a data-driven world.
Latest Posts
Latest Posts
-
An Alloy Consists Of Nickel Zinc And Copper
Mar 31, 2025
-
What Is The Potential Difference Across The 40 O Resistor
Mar 31, 2025
-
Look At The Figure Find The Length Of
Mar 31, 2025
-
What Is The Bond Order Of No
Mar 31, 2025
-
Two Small Metal Spheres Are Connected By A Wire
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Percent Of 12.5 Is 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
