What Is The Fraction For 0.85
News Leon
Apr 02, 2025 · 4 min read
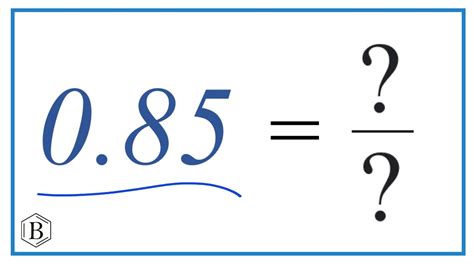
Table of Contents
What is the Fraction for 0.85? A Deep Dive into Decimal-to-Fraction Conversion
The simple question, "What is the fraction for 0.85?" might seem trivial at first glance. However, understanding the process of converting decimals to fractions is fundamental in mathematics and has wide-ranging applications in various fields. This comprehensive guide will not only answer this specific question but also explore the broader concept of decimal-to-fraction conversion, providing you with the knowledge and skills to tackle similar problems with confidence.
Understanding Decimals and Fractions
Before diving into the conversion process, let's refresh our understanding of decimals and fractions.
Decimals: Decimals are a way of representing numbers that are not whole numbers. They use a base-ten system, with each digit to the right of the decimal point representing a power of ten (tenths, hundredths, thousandths, and so on). For example, 0.85 represents 8 tenths and 5 hundredths.
Fractions: Fractions represent a part of a whole. They consist of two parts: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, ½ represents one out of two equal parts.
Converting 0.85 to a Fraction: A Step-by-Step Guide
The conversion of 0.85 to a fraction involves a straightforward process:
-
Identify the place value of the last digit: In 0.85, the last digit (5) is in the hundredths place. This means the denominator of our fraction will be 100.
-
Write the decimal as a fraction: The digits to the right of the decimal point become the numerator. Therefore, 0.85 becomes 85/100.
-
Simplify the fraction: This step is crucial for expressing the fraction in its simplest form. We need to find the greatest common divisor (GCD) of the numerator (85) and the denominator (100). The GCD of 85 and 100 is 5.
-
Divide both the numerator and denominator by the GCD: Dividing both 85 and 100 by 5, we get:
85 ÷ 5 = 17 100 ÷ 5 = 20
Therefore, the simplified fraction for 0.85 is 17/20.
Beyond 0.85: Mastering Decimal-to-Fraction Conversion
The method used to convert 0.85 to a fraction can be applied to any decimal number. Let's explore some examples:
Example 1: Converting 0.75 to a fraction
- The last digit is in the hundredths place, so the denominator is 100.
- The fraction is 75/100.
- The GCD of 75 and 100 is 25.
- Dividing both by 25 gives us 3/4.
Therefore, 0.75 = 3/4.
Example 2: Converting 0.6 to a fraction
- The last digit is in the tenths place, so the denominator is 10.
- The fraction is 6/10.
- The GCD of 6 and 10 is 2.
- Dividing both by 2 gives us 3/5.
Therefore, 0.6 = 3/5.
Example 3: Converting 0.125 to a fraction
- The last digit is in the thousandths place, so the denominator is 1000.
- The fraction is 125/1000.
- The GCD of 125 and 1000 is 125.
- Dividing both by 125 gives us 1/8.
Therefore, 0.125 = 1/8.
Example 4: Converting a recurring decimal to a fraction
Recurring decimals require a slightly different approach. Let's consider 0.333... (0.3 recurring).
- Let x = 0.333...
- Multiply both sides by 10: 10x = 3.333...
- Subtract the first equation from the second: 10x - x = 3.333... - 0.333... This simplifies to 9x = 3.
- Solve for x: x = 3/9, which simplifies to 1/3.
Therefore, 0.333... = 1/3.
Practical Applications of Decimal-to-Fraction Conversion
The ability to convert decimals to fractions is not merely an academic exercise. It has practical applications in various fields, including:
-
Cooking and Baking: Recipes often require precise measurements, and understanding fractions is essential for accurate conversions.
-
Engineering and Construction: Precise calculations are crucial, and converting decimals to fractions allows for greater accuracy in measurements and calculations.
-
Finance: Calculating interest rates and proportions often involves working with both decimals and fractions.
-
Science: Many scientific calculations require converting between decimals and fractions for accurate representation of data.
Tips and Tricks for Efficient Conversion
-
Memorize common conversions: Familiarize yourself with common decimal-to-fraction equivalents, such as 0.5 = ½, 0.25 = ¼, 0.75 = ¾, etc. This will speed up your calculations.
-
Use online calculators: Numerous online calculators are available to assist with decimal-to-fraction conversions, particularly for more complex numbers. However, understanding the underlying process is still vital.
-
Practice regularly: The more you practice converting decimals to fractions, the more proficient you will become.
Conclusion: Mastering the Art of Decimal-to-Fraction Conversion
Converting decimals to fractions is a fundamental mathematical skill with far-reaching applications. While the process may seem simple for numbers like 0.85, understanding the underlying principles and practicing various examples will equip you with the ability to confidently tackle more complex conversions. Remember that simplifying the fraction to its lowest terms is crucial for accurate representation. Mastering this skill will enhance your mathematical abilities and provide a solid foundation for tackling more advanced mathematical concepts. So, next time you encounter a decimal that needs converting, remember the steps outlined here, and you'll be well on your way to achieving accurate and efficient results.
Latest Posts
Latest Posts
-
Arrange The Following Radicals In Order Of Increasing Stability
Apr 03, 2025
-
The Programmer Usually Enters Source Code Into A Computer With
Apr 03, 2025
-
When Dissolved In Water Acids Produce
Apr 03, 2025
-
Which Chemical Equation Is Correctly Balanced
Apr 03, 2025
-
What Is The Overall Tone Of This Passage
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Fraction For 0.85 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
