What Is 4 To The Power Of 5
News Leon
Mar 28, 2025 · 5 min read
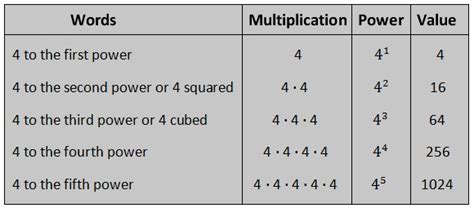
Table of Contents
What is 4 to the Power of 5? A Deep Dive into Exponentiation
This seemingly simple question, "What is 4 to the power of 5?", opens a door to a fascinating world of mathematics, specifically exponentiation. While the answer itself is straightforward to calculate, understanding the underlying concepts provides a powerful foundation for more complex mathematical operations and problem-solving. This article will not only answer the question but delve into the mechanics of exponentiation, its applications in various fields, and explore related mathematical concepts.
Understanding Exponentiation: Beyond Basic Arithmetic
Exponentiation, often represented by a superscript number (like the "5" in 4<sup>5</sup>), signifies repeated multiplication. It's a fundamental operation in mathematics, extending beyond simple addition, subtraction, multiplication, and division. In the expression 4<sup>5</sup>, the number 4 is called the base, and the number 5 is called the exponent or power. This means we're multiplying the base (4) by itself the number of times indicated by the exponent (5).
The Calculation: 4 to the Power of 5
To calculate 4<sup>5</sup>, we simply multiply 4 by itself five times:
4<sup>5</sup> = 4 × 4 × 4 × 4 × 4 = 1024
Therefore, 4 to the power of 5 is 1024. This is a relatively straightforward calculation, but the concept scales to much larger and more complex numbers.
Expanding the Understanding: Exploring Exponents
The exponent doesn't just dictate the number of multiplications; it reveals a pattern of exponential growth. Let's look at the progression of powers of 4:
- 4<sup>1</sup> = 4
- 4<sup>2</sup> = 16
- 4<sup>3</sup> = 64
- 4<sup>4</sup> = 256
- 4<sup>5</sup> = 1024
- 4<sup>6</sup> = 4096
Notice how rapidly the value increases. This exponential growth is crucial in understanding various phenomena across diverse fields, as we'll discuss later.
Negative Exponents: Inverting the Process
Exponentiation extends beyond positive integers. Negative exponents represent the reciprocal of the positive power. For example:
4<sup>-1</sup> = 1/4<sup>1</sup> = 1/4 = 0.25 4<sup>-2</sup> = 1/4<sup>2</sup> = 1/16 = 0.0625
This introduces the concept of fractions and decimals into the realm of exponentiation.
Fractional Exponents: Introducing Roots
Fractional exponents introduce the concept of roots. For instance:
4<sup>1/2</sup> represents the square root of 4, which is 2 (because 2 × 2 = 4). 4<sup>1/3</sup> represents the cube root of 4, which is approximately 1.587. 4<sup>3/2</sup> can be interpreted as (4<sup>1/2</sup>)<sup>3</sup> = 2<sup>3</sup> = 8 or as (4<sup>3</sup>)<sup>1/2</sup> = 64<sup>1/2</sup> = 8.
Fractional exponents elegantly connect exponentiation with roots, expanding the power and flexibility of the operation.
Zero Exponent: A Special Case
Any non-zero number raised to the power of zero equals 1. This might seem counterintuitive, but it's a consistent rule within the system of exponentiation.
4<sup>0</sup> = 1
This is a fundamental property that maintains consistency in mathematical operations and algebraic manipulations.
Applications of Exponentiation: Beyond the Classroom
The concept of 4<sup>5</sup>, and exponentiation in general, transcends abstract mathematical exercises. Its applications are widespread:
Compound Interest: The Power of Growth
In finance, compound interest utilizes exponentiation to model the growth of investments over time. The formula involves raising the principal amount to the power of the number of compounding periods. Understanding exponential growth is crucial for making sound financial decisions and projections.
Population Growth: Modeling Exponential Increases
Exponential functions are used extensively in modeling population growth. Whether it's human populations, bacterial colonies, or animal populations, the growth often follows an exponential pattern, making exponentiation a critical tool in biological modeling and forecasting.
Radioactive Decay: Modeling Exponential Decrease
Conversely, radioactive decay demonstrates exponential decrease. The amount of radioactive material remaining over time follows an exponential decay pattern. This is important in various fields, including medicine, environmental science, and nuclear physics.
Computer Science: Bits and Bytes
In computer science, exponentiation is fundamental to understanding binary systems. The base-2 system (powers of 2) underpins the representation of data in computers, with bits and bytes being powers of 2.
Physics: Exponential Phenomena
Many physical phenomena exhibit exponential behavior. For example, the intensity of light decreases exponentially with distance, and the cooling of an object often follows an exponential decay pattern.
Expanding on the Concept: Related Mathematical Concepts
Understanding 4<sup>5</sup> leads to a broader comprehension of various related mathematical topics:
Logarithms: The Inverse Operation
Logarithms are the inverse operation of exponentiation. If 4<sup>5</sup> = 1024, then the logarithm base 4 of 1024 is 5. Logarithms are essential in various applications, including solving exponential equations and simplifying complex calculations.
Scientific Notation: Expressing Very Large or Small Numbers
Scientific notation uses exponentiation to represent extremely large or small numbers in a concise manner. This is crucial in scientific fields dealing with vast scales, such as astronomy or particle physics.
Polynomials and Series: Building Complex Functions
Exponentiation is a building block for more complex mathematical expressions, including polynomials and infinite series. These concepts are fundamental in calculus and advanced mathematics.
Conclusion: The Significance of a Simple Calculation
While the answer to "What is 4 to the power of 5?" is simply 1024, the journey to that answer unlocks a wealth of knowledge about exponentiation, its implications, and its profound applications across diverse disciplines. Understanding this seemingly simple calculation provides a foundational understanding of exponential growth and decay, impacting our understanding of finance, biology, physics, and computer science, among many other fields. The concept extends far beyond a simple arithmetic operation, highlighting the interconnectedness and power of mathematical principles. This exploration encourages further investigation into the fascinating world of mathematics and its crucial role in our comprehension of the world around us.
Latest Posts
Latest Posts
-
What Is The Number Of Protons For Magnesium
Mar 31, 2025
-
Each Hemoglobin Molecule Can Carry How Many Oxygen Molecules
Mar 31, 2025
-
Oxidation State Of O In Oh
Mar 31, 2025
-
Orbitals That Have The Same Energy Are Called
Mar 31, 2025
-
Sugar Dissolve In Water Physical Or Chemical
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 4 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
