What Are The Coordinates Of Point Q
News Leon
Mar 28, 2025 · 6 min read
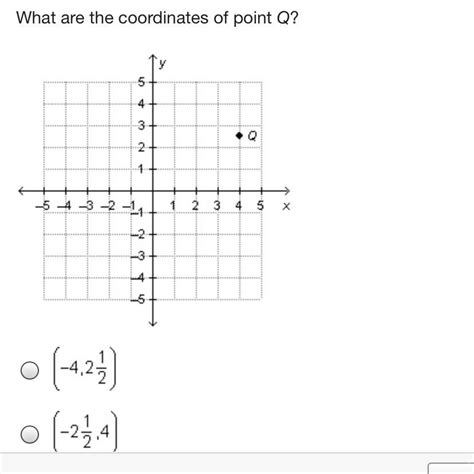
Table of Contents
What Are the Coordinates of Point Q? A Comprehensive Guide to Coordinate Geometry
Determining the coordinates of a point, particularly a point labeled 'Q', requires understanding the fundamental principles of coordinate geometry. This comprehensive guide will delve into various methods to find the coordinates of point Q, covering different scenarios and complexities. We'll explore methods applicable to different geometric shapes and situations, providing a solid foundation for anyone tackling coordinate geometry problems.
Understanding Coordinate Systems
Before diving into finding the coordinates of point Q, let's establish a clear understanding of coordinate systems. The most commonly used is the Cartesian coordinate system, also known as the rectangular coordinate system. This system uses two perpendicular lines, the x-axis (horizontal) and the y-axis (vertical), to define a plane. The point where these axes intersect is called the origin (0, 0).
Every point on the plane is uniquely identified by an ordered pair (x, y), where 'x' represents the horizontal distance from the origin and 'y' represents the vertical distance from the origin. Positive x values are to the right of the origin, negative x values to the left. Positive y values are above the origin, and negative y values are below.
Methods for Finding the Coordinates of Point Q
The method for finding the coordinates of point Q depends heavily on the context of the problem. Here are several common scenarios:
1. Point Q given directly:
The simplest scenario is when the coordinates of point Q are explicitly stated in the problem. For instance, the problem might say, "Point Q has coordinates (3, -2)." In this case, the coordinates are readily available and no further calculation is needed.
2. Point Q defined by a graph:
If point Q is plotted on a graph, its coordinates can be easily read directly from the graph. Locate point Q on the graph, and trace a perpendicular line down to the x-axis to find the x-coordinate and a perpendicular line across to the y-axis to find the y-coordinate. For example, if the perpendicular line to the x-axis intersects at 4 and the perpendicular line to the y-axis intersects at 2, then the coordinates of Q are (4, 2).
3. Point Q defined by geometric relationships:
This is where the problem becomes more challenging. We often need to use geometric properties and formulas to find the coordinates of Q. Several examples follow:
-
Midpoint Formula: If point Q is the midpoint of a line segment with endpoints A(x₁, y₁) and B(x₂, y₂), then the coordinates of Q are given by the midpoint formula:
Q(x, y) = ((x₁ + x₂)/2, (y₁ + y₂)/2)
This formula averages the x-coordinates and the y-coordinates of the endpoints to find the midpoint.
-
Section Formula: If point Q divides a line segment AB in the ratio m:n, then the coordinates of Q are given by the section formula:
Q(x, y) = ((mx₂ + nx₁)/(m + n), (my₂ + ny₁)/(m + n))
This formula is a generalization of the midpoint formula (where m = n = 1). Understanding the ratio is crucial for applying this formula correctly.
-
Point Q as a vertex of a polygon: If point Q is a vertex of a polygon (triangle, quadrilateral, etc.), and the coordinates of the other vertices are known, we may be able to use various geometric properties to deduce the coordinates of Q. For instance, if Q is a vertex of a right-angled triangle, we can use Pythagorean theorem or trigonometric ratios to find its coordinates, provided enough information about the other vertices and sides is given.
-
Point Q defined by equations of lines: If point Q lies on the intersection of two lines, its coordinates can be found by solving the system of equations representing those lines. For example, if Q lies on the lines y = 2x + 1 and y = -x + 4, we can solve the system:
2x + 1 = -x + 4 3x = 3 x = 1
Substitute x = 1 into either equation to find y: y = 2(1) + 1 = 3
Therefore, the coordinates of Q are (1, 3).
-
Point Q defined by transformations: If point Q is obtained by applying a geometric transformation (translation, rotation, reflection, dilation) to another point whose coordinates are known, we can use the transformation rules to find the coordinates of Q. For example, a translation by vector (a, b) shifts a point (x, y) to (x + a, y + b). Rotations and reflections are more complex and involve trigonometric functions.
4. Point Q in three-dimensional space:
Extending to three dimensions, we use a three-dimensional coordinate system with x, y, and z axes. Points are represented by ordered triples (x, y, z). The methods described above can be extended to three dimensions, but the calculations become more involved. For instance, the midpoint formula becomes:
Q(x, y, z) = ((x₁ + x₂)/2, (y₁ + y₂)/2, (z₁ + z₂)/2)
Advanced Techniques and Considerations
-
Vectors: Vectors provide a powerful tool for solving coordinate geometry problems. A vector can represent the displacement between two points. Vector addition, subtraction, and scalar multiplication can be used to find the coordinates of points based on their relationships with other points.
-
Matrices: Matrices can be used to represent geometric transformations, making complex transformations easier to compute. This is particularly useful when dealing with multiple points or complex sequences of transformations.
-
Software and Tools: Various software programs and online tools are available to assist with coordinate geometry calculations, especially for more complex problems or large datasets. These tools can automate calculations and create visualizations to aid understanding.
Practical Examples
Let's work through a few examples to solidify our understanding:
Example 1: Find the coordinates of point Q, which is the midpoint of the line segment connecting A(2, 5) and B(8, 1).
Using the midpoint formula:
Q(x, y) = ((2 + 8)/2, (5 + 1)/2) = (5, 3)
Example 2: Point Q divides the line segment AB in the ratio 2:3, where A(1, 4) and B(7, -2). Find the coordinates of Q.
Using the section formula:
Q(x, y) = ((27 + 31)/(2 + 3), (2*-2 + 3*4)/(2 + 3)) = ((14 + 3)/5, (-4 + 12)/5) = (17/5, 8/5)
Example 3: Point Q lies on the intersection of the lines y = x + 2 and y = -2x + 8. Find its coordinates.
Solving the system of equations:
x + 2 = -2x + 8 3x = 6 x = 2
Substitute x = 2 into either equation: y = 2 + 2 = 4
Therefore, Q(2, 4).
Conclusion
Finding the coordinates of point Q involves understanding the coordinate system and applying relevant geometric principles and formulas. The specific method depends on the context of the problem. From simple direct statements to complex geometric relationships and transformations, mastering these techniques equips you to effectively solve a wide range of coordinate geometry problems. Remember to carefully analyze the given information, choose the appropriate method, and perform the calculations accurately. Practicing with diverse problems is key to building proficiency in coordinate geometry. This guide provides a strong foundation; further exploration of advanced techniques and the use of software tools can enhance your problem-solving skills even further.
Latest Posts
Latest Posts
-
An Alloy Consists Of Nickel Zinc And Copper
Mar 31, 2025
-
What Is The Potential Difference Across The 40 O Resistor
Mar 31, 2025
-
Look At The Figure Find The Length Of
Mar 31, 2025
-
What Is The Bond Order Of No
Mar 31, 2025
-
Two Small Metal Spheres Are Connected By A Wire
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are The Coordinates Of Point Q . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
