Two Cables Are Tied Together At C
News Leon
Mar 28, 2025 · 6 min read
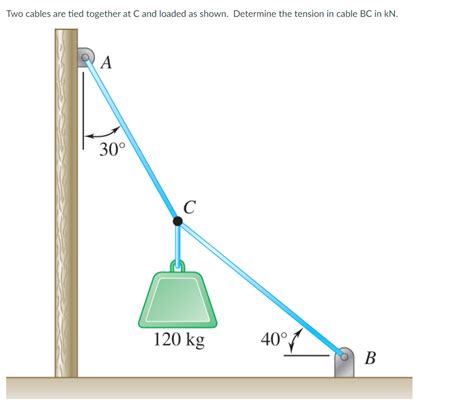
Table of Contents
Two Cables Tied Together at C: A Comprehensive Analysis of Static Equilibrium
The seemingly simple scenario of two cables tied together at a point C presents a rich opportunity to explore fundamental concepts in physics, particularly static equilibrium and vector analysis. This article delves into the intricacies of this problem, examining different aspects, including force analysis, solving techniques, and practical applications. We'll dissect the problem from various angles, providing a comprehensive understanding suitable for students, engineers, and anyone curious about the principles of statics.
Understanding Static Equilibrium
Before diving into the specifics of two cables tied at point C, let's establish a firm grasp of static equilibrium. An object is said to be in static equilibrium when it is at rest and remains at rest. This seemingly straightforward statement encapsulates two crucial conditions:
-
Translational Equilibrium: The net force acting on the object is zero. This means the vector sum of all forces acting on the object must equal zero. Mathematically, this is represented as ΣF = 0.
-
Rotational Equilibrium: The net moment (torque) acting on the object is zero. This means the sum of all moments about any point must be zero. Mathematically, this is represented as ΣM = 0.
These two conditions are crucial for maintaining static equilibrium. Violation of either condition will result in the object accelerating, either linearly or rotationally.
The Two-Cable System: A Detailed Breakdown
Consider two cables, Cable A and Cable B, tied together at point C. Each cable is subjected to a tension force, T<sub>A</sub> and T<sub>B</sub> respectively. These tension forces act along the respective cable directions. Often, a weight or load (W) is suspended from point C, adding another force to the system. The system is in static equilibrium if the forces balance each other out.
Force Diagrams: The Key to Solving the Problem
The first and most crucial step in analyzing this system is to draw a free-body diagram (FBD). A FBD is a simplified representation of the object (point C in our case) showing only the forces acting upon it. It's essential to accurately represent the direction and magnitude of each force.
For our two-cable system, the FBD will include:
- T<sub>A</sub>: The tension force in Cable A, acting along the direction of Cable A.
- T<sub>B</sub>: The tension force in Cable B, acting along the direction of Cable B.
- W: The weight suspended from point C, acting vertically downwards.
These forces form a closed vector polygon. In other words, if you draw these vectors head-to-tail, they should form a closed triangle (or a closed polygon if more forces are involved). This visual representation confirms the condition of translational equilibrium (ΣF = 0).
Solving for Unknowns: Techniques and Approaches
The most common methods to solve for the unknown tension forces (T<sub>A</sub> and T<sub>B</sub>) and potentially the weight (W) if it's unknown, involve vector analysis and trigonometry. Here are two common approaches:
1. Resolving Forces into Components: This method involves resolving each force into its horizontal (x) and vertical (y) components. By applying the conditions of static equilibrium (ΣF<sub>x</sub> = 0 and ΣF<sub>y</sub> = 0), we obtain two equations with two unknowns (typically T<sub>A</sub> and T<sub>B</sub>). Solving these simultaneous equations yields the magnitudes of the tension forces.
2. Using the Law of Sines and Cosines: If the angles between the cables and the vertical are known, we can directly apply the Law of Sines and Cosines to the force triangle formed by T<sub>A</sub>, T<sub>B</sub>, and W. This approach is particularly useful when dealing with graphical solutions or when working with angles rather than components.
Example Problem:
Let's consider a practical example. Two cables are tied together at point C. Cable A makes an angle of 30 degrees with the horizontal, and Cable B makes an angle of 45 degrees with the horizontal. A weight of 100N is suspended from point C. Find the tension in each cable.
By resolving forces into components and applying the equilibrium conditions, we can solve for T<sub>A</sub> and T<sub>B</sub>. The solution will involve trigonometric functions (sine and cosine) applied to the angles and the known weight. The detailed calculation is left as an exercise to the reader, but the approach involves constructing and solving simultaneous equations based on the horizontal and vertical equilibrium conditions.
Advanced Considerations and Real-world Applications
The basic two-cable system described above serves as a foundation for understanding more complex scenarios. Let's explore some advanced considerations and real-world applications:
Multiple Cables and Loads: Extending the Analysis
The principles discussed can be extended to systems with multiple cables and loads. The process remains the same: draw a free-body diagram, resolve forces into components, and apply the equilibrium equations. However, the number of equations and unknowns will increase with the complexity of the system. For instance, with three cables and a load, we will have three unknowns (tensions in each cable) and therefore need three independent equations to solve the system. Matrix methods can be efficiently utilized for solving such systems with a large number of unknowns.
Cable Sag and Elasticity: Real-World Effects
In real-world scenarios, cables exhibit sag (due to their own weight) and elasticity (stretching under tension). These factors introduce additional complexities to the analysis. Accounting for cable sag requires advanced techniques involving catenary curves, while considering cable elasticity demands incorporating material properties and stress-strain relationships into the calculations. Specialized software is often employed for accurate analysis in these cases.
Applications in Engineering and Structural Analysis
The analysis of two cables tied together is fundamental to many engineering applications:
-
Bridge Design: Suspension bridges rely on the principles of cable tension to support the deck. The analysis of cable forces is crucial in designing safe and stable structures.
-
Electrical Transmission Lines: Understanding cable tension is critical in designing and maintaining electrical transmission lines. Sag and wind load considerations are essential for preventing cable failure.
-
Crane Systems: Crane systems utilize cables to lift and move heavy loads. Accurate calculation of cable tensions is paramount for ensuring the safe operation of these systems.
-
Structural Support Systems: In various structures, cable systems are used for bracing and support. Correctly analyzing cable forces ensures the stability and integrity of these structures.
-
Aerospace Engineering: Analyzing tension in cables is crucial for the design of deployable structures such as antennas and solar panels for spacecraft, and for the design and testing of parachute systems.
Conclusion: Mastering the Fundamentals
Understanding the principles of static equilibrium and applying them to the seemingly simple system of two cables tied together at a point is fundamental to a grasp of mechanics and numerous engineering applications. Through the careful construction of free-body diagrams, the application of vector analysis or trigonometry, and the consideration of equilibrium conditions, we can confidently solve for unknown forces and gain crucial insights into the behavior of these systems. While the basic system offers a starting point, this article highlights the complexity and diversity of applications that stem from understanding this fundamental problem, paving the way for analyzing even more intricate structures and scenarios. Remember, mastering these fundamental principles is crucial for success in engineering and related fields. Continuous practice and exploration of various problems will solidify understanding and build expertise in this area.
Latest Posts
Latest Posts
-
Which Type Of Muscle Tissue Is Multinucleated
Mar 31, 2025
-
True Or False Evaporation Is A Physical Change
Mar 31, 2025
-
Do Gram Positive Bacteria Have Porins
Mar 31, 2025
-
Which Of The Following Compounds Is Most Soluble In Water
Mar 31, 2025
-
Part Of The Brain That Controls Breathing And Heartbeat
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Two Cables Are Tied Together At C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
