Right Hand Rule For Angular Velocity
News Leon
Mar 31, 2025 · 6 min read
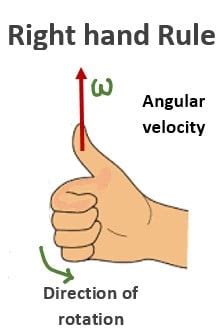
Table of Contents
Right-Hand Rule for Angular Velocity: A Comprehensive Guide
The right-hand rule is a fundamental concept in physics, particularly in mechanics and electromagnetism. Understanding this rule is crucial for correctly determining the direction of various vector quantities, including angular velocity. This comprehensive guide delves into the intricacies of the right-hand rule as it applies to angular velocity, providing a clear understanding with numerous examples and applications.
What is Angular Velocity?
Before diving into the right-hand rule, let's establish a clear understanding of angular velocity. Angular velocity (ω, omega) is a vector quantity that describes the rate of change of angular displacement of a rotating object. It quantifies how quickly an object rotates around a chosen axis. Unlike linear velocity, which describes the rate of change of position in a straight line, angular velocity describes rotational motion. It's measured in radians per second (rad/s) or revolutions per minute (rpm).
Key Characteristics of Angular Velocity:
- Magnitude: Represents the speed of rotation. A higher magnitude indicates faster rotation.
- Direction: Points along the axis of rotation. This is where the right-hand rule comes into play.
- Units: Radians per second (rad/s) or revolutions per minute (rpm).
Understanding the Right-Hand Rule for Angular Velocity
The right-hand rule provides a simple yet effective method for determining the direction of the angular velocity vector. The process is as follows:
-
Identify the axis of rotation: Determine the line around which the object is rotating. This is the axis of rotation.
-
Curl your fingers: Curl the fingers of your right hand in the direction of the object's rotation. Imagine 'grasping' the axis of rotation with your hand.
-
Extend your thumb: Extend your thumb. The direction your thumb points represents the direction of the angular velocity vector (ω).
Visualizing the Right-Hand Rule
Imagine a spinning top. If the top spins clockwise as viewed from above, curl your right-hand fingers in the clockwise direction. Your thumb will then point downwards, indicating that the angular velocity vector points downwards. Conversely, if the top spins counter-clockwise, your thumb will point upwards.
This seemingly simple rule has profound implications for understanding the dynamics of rotating systems. It allows us to assign a direction to a rotational motion, a concept crucial for applying more advanced physics principles.
Applications of the Right-Hand Rule in Angular Velocity
The right-hand rule isn't just a theoretical concept; it finds widespread applications in various fields of physics and engineering. Here are a few examples:
1. Rotational Dynamics: Torque and Angular Acceleration
The right-hand rule plays a vital role in understanding the relationship between torque (τ), angular momentum (L), and angular acceleration (α). Torque, the rotational equivalent of force, causes a change in angular momentum. The direction of the torque vector is determined using the right-hand rule:
- Curl your fingers: in the direction of the rotational effect of the applied force.
- Thumb: points in the direction of the torque vector.
Similarly, angular acceleration, the rate of change of angular velocity, also follows the right-hand rule. The direction of angular acceleration is consistent with the direction of the net torque acting on the object.
2. Rigid Body Dynamics
In rigid body dynamics, the right-hand rule is crucial for analyzing the motion of complex objects rotating around multiple axes. It allows us to systematically decompose the motion into components and apply the principles of rotational mechanics. For example, in analyzing the motion of a gyroscope, the right-hand rule helps determine the direction of the precession and nutation.
3. Angular Momentum
Angular momentum (L) is a measure of an object's rotational inertia. Similar to torque and angular acceleration, the direction of the angular momentum vector is determined using the right-hand rule. The magnitude of angular momentum is dependent on both the moment of inertia and the angular velocity. Understanding the direction of angular momentum is crucial for understanding the conservation of angular momentum principle – a cornerstone of classical mechanics.
4. Electromagnetism: Magnetic Fields and Forces on Moving Charges
While primarily associated with mechanics, the right-hand rule also has significant applications in electromagnetism. When a charged particle moves through a magnetic field, it experiences a force. The direction of this force is determined using a variation of the right-hand rule, often referred to as the "right-hand rule for magnetic force":
- Thumb: points in the direction of the velocity of the charged particle.
- Fingers: point in the direction of the magnetic field.
- Palm: the direction of the force on a positive charge is indicated by the palm. The force on a negative charge is in the opposite direction.
This rule is fundamental for understanding electric motors, generators, and other electromagnetic devices.
5. Fluid Dynamics: Vorticity
In fluid dynamics, vorticity is a measure of the local rotation of a fluid element. The vorticity vector is determined using the right-hand rule, pointing in the direction of the axis of rotation of the fluid element. Understanding vorticity is crucial for modeling and understanding fluid flow patterns, especially in complex turbulent flows.
Common Misconceptions and Troubleshooting
While the right-hand rule seems straightforward, certain misconceptions can lead to errors.
-
Left-hand rule: Always use your right hand! The right-hand rule is specific to the convention used in physics.
-
Confusing rotation and axis: Carefully identify the axis of rotation before applying the rule. The direction of rotation is crucial for determining the direction of the angular velocity vector.
-
Three-dimensional visualization: Visualizing the three-dimensional nature of the vectors can be challenging. Practice with various examples to improve your spatial reasoning skills.
Advanced Applications and Extensions
The right-hand rule forms the foundation for understanding more advanced concepts like:
-
Cross products: The angular velocity vector is often expressed as the cross product of two other vectors (like position and linear velocity). The right-hand rule directly relates to the direction of the cross product.
-
Tensor calculus: In more advanced treatments of rotational motion, tensor calculus extends the concepts of vectors and the right-hand rule to handle more complex rotations and deformations.
-
Relativistic effects: Although the right-hand rule is primarily a classical concept, it still provides a useful approximation for many relativistic scenarios involving rotating systems.
Conclusion: Mastering the Right-Hand Rule
The right-hand rule for angular velocity is an indispensable tool for anyone studying physics, engineering, or related fields. Mastering this rule is crucial for correctly analyzing and predicting the behavior of rotating systems. By understanding the underlying principles and practicing with various examples, you can confidently apply this fundamental concept to a wide range of applications. Remember to practice visualization and address any misconceptions early on to ensure accurate and efficient problem-solving. The consistent application of the right-hand rule will solidify your understanding of rotational motion and open doors to more advanced concepts in physics and beyond.
Latest Posts
Latest Posts
-
Adjacent Angles Whose Sum In 180 Degrees
Apr 01, 2025
-
Lewis Dot Structure For Magnesium Chloride
Apr 01, 2025
-
A Group Of Related Records Is Called A Table
Apr 01, 2025
-
Provides Long Term Energy Storage For Animals
Apr 01, 2025
-
The Average Propensity To Consume Refers To
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Right Hand Rule For Angular Velocity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
