Integral Of 1 Square Root Of A 2 X 2
News Leon
Mar 29, 2025 · 5 min read
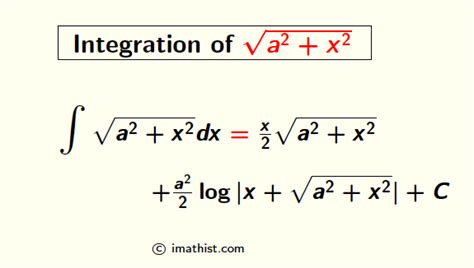
Table of Contents
The Indefinite Integral of 1/√(a²x² + 2bx + c)
The indefinite integral ∫ 1/√(a²x² + 2bx + c) dx presents a classic challenge in calculus. This seemingly simple expression requires careful consideration and a strategic approach to solve. This comprehensive guide will dissect this integral, exploring various methods and providing a deep understanding of the underlying concepts. We'll delve into specific cases, address potential difficulties, and offer practical techniques to tackle similar problems.
Understanding the Problem
The integrand, 1/√(a²x² + 2bx + c), represents a general form of an integral often encountered in various applications of mathematics, physics, and engineering. The solution depends critically on the values of the coefficients a, b, and c. The discriminant (b² - a²c) plays a crucial role in determining the appropriate solution method.
Case 1: a = 0
If 'a' equals zero, the integral simplifies considerably:
∫ 1/√(2bx + c) dx
This is a straightforward case, solvable using a simple u-substitution. Let u = 2bx + c, then du = 2b dx. The integral becomes:
(1/2b) ∫ u⁻¹/² du = (1/2b) * 2u¹/² + C = √(2bx + c)/b + C
Where C is the constant of integration.
Case 2: a ≠ 0; Discriminant Analysis
When 'a' is non-zero, the nature of the quadratic expression (a²x² + 2bx + c) determines the solution strategy. The discriminant, Δ = b² - a²c, is the key factor:
1. Δ > 0 (Positive Discriminant):
When the discriminant is positive, the quadratic expression has two distinct real roots. This case requires completing the square to transform the integrand into a form amenable to a trigonometric substitution.
Let's complete the square:
a²x² + 2bx + c = a² (x² + (2b/a²)x) + c = a² (x + b/a²)² - b²/a² + c
Now rewrite the integral:
∫ 1/√(a² (x + b/a²)² - (b² - a²c)/a²) dx
We use the substitution:
x + b/a² = (√(b² - a²c)/a²) sec(θ)
dx = (√(b² - a²c)/a²) sec(θ) tan(θ) dθ
Substituting these into the integral leads to a manageable trigonometric integral that can be solved using standard trigonometric identities. The final answer will involve inverse hyperbolic functions or logarithmic functions, depending on the specific values of a, b, and c.
2. Δ = 0 (Zero Discriminant):
A zero discriminant indicates a perfect square. The quadratic expression can be factored into (ax + k)², where k is a constant. The integral then becomes:
∫ 1/√((ax + k)²) dx = ∫ 1/(|ax + k|) dx
This integral is relatively easy to solve using another u-substitution:
Let u = ax + k, then du = a dx. The integral becomes:
(1/a) ∫ 1/|u| du = (1/a) ln|u| + C = (1/a) ln|ax + k| + C
However, remember that the absolute value is crucial to handle both positive and negative values of (ax + k).
3. Δ < 0 (Negative Discriminant):
A negative discriminant means that the quadratic expression has no real roots. The quadratic is always positive (assuming a² > 0). The appropriate substitution involves inverse trigonometric functions. The steps involve completing the square, as in the positive discriminant case, but the substitution will involve trigonometric functions, ultimately leading to an inverse trigonometric function in the solution. The specific trigonometric substitution will depend on how you complete the square and the resulting form of the quadratic.
For example, if the completed square is of the form a²(x + p)² + q², you'd use a substitution involving tan θ or sin θ to simplify the integral. This usually results in an inverse sine or inverse tangent function in the final solution.
Detailed Example: Δ > 0
Let's solve a specific example with a positive discriminant:
∫ 1/√(4x² + 8x + 3) dx
- Complete the square:
4x² + 8x + 3 = 4(x² + 2x) + 3 = 4(x + 1)² - 1
- Rewrite the integral:
∫ 1/√(4(x + 1)² - 1) dx
- Substitution:
Let x + 1 = (1/2) sec(θ) dx = (1/2) sec(θ) tan(θ) dθ
Substituting this results in:
∫ (1/2) sec(θ) tan(θ) / √(sec²(θ) - 1) dθ = ∫ (1/2) sec(θ) dθ
- Solve the Trigonometric Integral:
∫ (1/2) sec(θ) dθ = (1/2) ln|sec(θ) + tan(θ)| + C
- Back-Substitute:
Since x + 1 = (1/2) sec(θ), sec(θ) = 2(x + 1). Using trigonometric identities, we can find tan(θ). The final solution would then be expressed in terms of x.
Handling Different Forms
The techniques outlined above can be adapted to handle slightly different forms of the integral. For example, if the integral is multiplied by a constant, or if there's a constant term outside the square root, you can adjust the steps accordingly. The core strategies of completing the square, making appropriate substitutions, and utilizing trigonometric identities remain essential.
Practical Tips and Considerations
- Always check the discriminant: This is the most crucial step. It immediately directs you to the most efficient solution method.
- Careful with substitutions: Ensure you correctly substitute back into x after solving the simplified integral.
- Absolute value signs: Remember to include absolute value signs whenever dealing with logarithms of expressions that could potentially be negative.
- Computational tools: For complex integrals or situations involving complicated numbers, consider using computational tools to verify your solution or to help in the integration process.
Conclusion
Solving the integral ∫ 1/√(a²x² + 2bx + c) dx is a multifaceted problem requiring a strong understanding of calculus techniques. The discriminant is the key to choosing the appropriate method, leading to either straightforward u-substitutions, or more complex trigonometric substitutions involving inverse hyperbolic or trigonometric functions. By carefully following the steps outlined and understanding the underlying principles, one can successfully tackle this integral and similar problems in calculus. The detailed examples and explanations provided in this guide should serve as valuable tools for further practice and application in related mathematical contexts. Remember to always double-check your work and utilize computational tools where appropriate for complex integrals.
Latest Posts
Latest Posts
-
Which Type Of Electromagnetic Wave Has The Shortest Wavelength
Apr 01, 2025
-
Which Of The Following Is True About Monopolistic Competition
Apr 01, 2025
-
Which Of The Following Is The Site Of Translation
Apr 01, 2025
-
What Is The Atomic Number Of An Atom Equal To
Apr 01, 2025
-
Parathyroid Hormone Does All Of The Following Except
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 Square Root Of A 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
