How Many Vertices Does Octagon Have
News Leon
Apr 02, 2025 · 5 min read
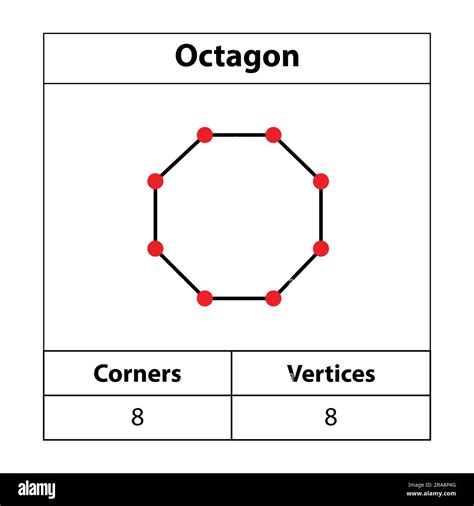
Table of Contents
How Many Vertices Does an Octagon Have? A Deep Dive into Octagonal Geometry
The question, "How many vertices does an octagon have?" might seem trivially simple at first glance. The answer, of course, is eight. However, understanding the properties of an octagon goes far beyond simply counting its vertices. This article delves deep into the fascinating world of octagons, exploring their various types, properties, applications, and their significance in mathematics and beyond. We'll unravel the intricacies of octagonal geometry, moving beyond the basic answer to provide a comprehensive understanding of this significant shape.
Understanding the Basics: Defining an Octagon
Before we delve into the complexities, let's establish a firm foundation. An octagon is a polygon, meaning it's a two-dimensional closed shape with straight sides. Crucially, an octagon has eight sides, and consequently, eight angles and eight vertices. A vertex, also known as a corner or node, is a point where two sides meet. Therefore, the answer to our initial question is confirmed: an octagon possesses eight vertices.
Types of Octagons: Beyond the Simple Definition
While the basic definition of an octagon is straightforward, understanding the different types of octagons adds depth and complexity. Octagons can be categorized based on their properties:
-
Regular Octagon: A regular octagon is a perfectly symmetrical octagon where all eight sides are of equal length, and all eight angles are equal. Each internal angle measures 135 degrees. This is the type of octagon most commonly visualized.
-
Irregular Octagon: An irregular octagon has sides of varying lengths and angles of varying measures. The possibilities for irregular octagons are virtually limitless.
-
Convex Octagon: In a convex octagon, all interior angles are less than 180 degrees. This means that all the vertices point outwards, creating a shape that doesn't "cave in" on itself. Both regular and many irregular octagons fall under this category.
-
Concave Octagon: A concave octagon has at least one interior angle greater than 180 degrees. This creates a shape where at least one part of the octagon points inwards.
Exploring Octagonal Properties: Angles, Diagonals, and Area
The properties of an octagon, particularly a regular octagon, are rich and mathematically significant. Let's explore some key characteristics:
Internal Angles: The Sum and Individual Measures
The sum of the internal angles of any polygon can be calculated using the formula: (n-2) * 180 degrees, where 'n' is the number of sides. For an octagon (n=8), the sum of its internal angles is (8-2) * 180 = 1080 degrees. In a regular octagon, each internal angle measures 1080/8 = 135 degrees.
Diagonals: Connecting the Vertices
Diagonals are line segments connecting non-adjacent vertices within a polygon. The number of diagonals in a polygon with 'n' sides is given by the formula: n(n-3)/2. For an octagon (n=8), the number of diagonals is 8(8-3)/2 = 20. These diagonals create a complex interplay within the octagon, dividing it into smaller triangles and quadrilaterals.
Area Calculation: Different Approaches
Calculating the area of a regular octagon can be done in several ways. One common method involves dividing the octagon into eight congruent isosceles triangles, finding the area of one triangle, and multiplying by eight. Alternatively, you can use the formula: A = 2(1 + √2)a², where 'a' is the length of a side. For irregular octagons, the area calculation becomes more complex and often requires breaking it down into smaller, simpler shapes.
Octagons in the Real World: Applications and Significance
Octagons, while not as ubiquitous as squares or triangles, appear in various aspects of our world, demonstrating their practical and aesthetic value.
Architectural Marvels: From Stop Signs to Buildings
The most recognizable example of an octagon in everyday life is the stop sign. The octagonal shape is instantly recognizable and commands attention, making it highly effective for its purpose. Beyond stop signs, octagonal shapes can be found in various architectural designs, sometimes as a decorative element or structural component. Some buildings incorporate octagonal structures or motifs, adding a unique visual appeal.
Nature's Geometry: Unexpected Octagonal Forms
While less common than other shapes in nature, octagonal patterns can occasionally be observed in crystal structures and certain plant formations. These natural occurrences demonstrate the mathematical principles underlying octagonal geometry even in the organic world.
Games and Puzzles: Octagons in Recreational Activities
Octagons play a role in several games and puzzles. Certain board games or tile-based puzzles might utilize octagonal pieces or layouts. The unique properties of the octagon can lend themselves to creating interesting challenges and strategies within these activities.
Expanding Our Understanding: Beyond the Basics
The exploration of octagons extends beyond simple geometric calculations. Understanding their symmetries, transformations, and relationships to other shapes enriches our mathematical knowledge and appreciation of geometry.
Symmetries and Transformations: Exploring Geometric Properties
Regular octagons exhibit a high degree of symmetry. They possess rotational symmetry of order 8, meaning they can be rotated eight times about their center and still look the same. They also have eight lines of reflectional symmetry, further demonstrating their symmetrical nature. Understanding these symmetries allows for a deeper appreciation of the octagon's inherent structure and beauty.
Relationship to Other Shapes: Connections and Transformations
Octagons are related to other polygons, particularly those with even numbers of sides. For example, an octagon can be divided into smaller squares, rectangles, or triangles, demonstrating its connections to simpler shapes. By exploring these relationships, we gain a more complete understanding of the octagon's place within the broader world of geometry.
Conclusion: The Enduring Significance of the Octagon
We began with a simple question: How many vertices does an octagon have? The answer, eight, is the foundation upon which we've built a more comprehensive exploration of octagonal geometry. From the basic definition to the intricate properties, real-world applications, and deeper mathematical connections, the octagon reveals itself to be a fascinating and important shape. Its symmetrical beauty and practical uses continue to capture our attention, underscoring its enduring significance in mathematics, architecture, and beyond. The next time you see an octagon, remember the rich tapestry of geometric properties and applications that lie beneath its eight vertices and sides.
Latest Posts
Latest Posts
-
Which Of The Following Is The Correct Accounting Equation
Apr 03, 2025
-
Check If Number Is Negative Python
Apr 03, 2025
-
What Is The Measure Of Angle Cbd
Apr 03, 2025
-
What Is The Equivalent Capacitance Of The Four Capacitors
Apr 03, 2025
-
Which Of The Following Is Not A Primary Air Pollutant
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How Many Vertices Does Octagon Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
