What Is The Measure Of Angle Cbd
News Leon
Apr 03, 2025 · 5 min read
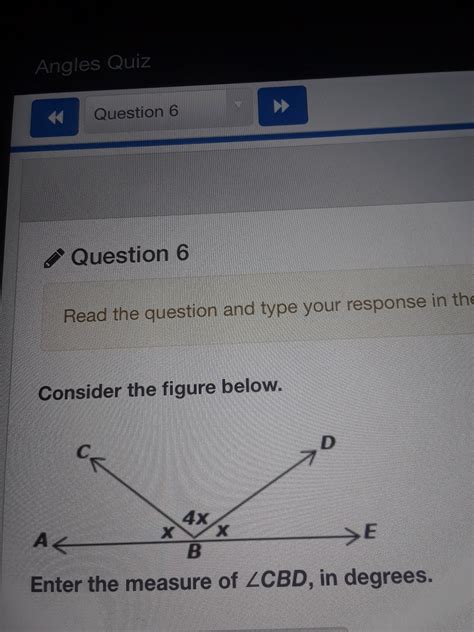
Table of Contents
What is the Measure of Angle CBD? A Comprehensive Guide to Geometry
Determining the measure of an angle, such as angle CBD, requires a systematic approach and a thorough understanding of geometric principles. This comprehensive guide will explore various methods for finding the measure of angle CBD, depending on the context provided – whether it's within a triangle, a quadrilateral, or a more complex geometric figure. We'll delve into different theorems, postulates, and problem-solving strategies, equipping you with the knowledge to tackle a wide array of angle measurement problems.
Understanding the Basics: Angles and Their Properties
Before we delve into the specifics of measuring angle CBD, let's refresh our understanding of fundamental concepts related to angles:
Types of Angles:
- Acute Angle: An angle measuring less than 90 degrees.
- Right Angle: An angle measuring exactly 90 degrees.
- Obtuse Angle: An angle measuring more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle measuring exactly 180 degrees.
- Reflex Angle: An angle measuring more than 180 degrees but less than 360 degrees.
Angle Relationships:
- Complementary Angles: Two angles whose measures add up to 90 degrees.
- Supplementary Angles: Two angles whose measures add up to 180 degrees.
- Vertical Angles: Two angles formed by intersecting lines that are opposite each other. They are always congruent (equal in measure).
- Adjacent Angles: Two angles that share a common vertex and side.
Methods for Determining the Measure of Angle CBD
The approach to finding the measure of angle CBD depends heavily on the given information. Let's explore various scenarios:
Scenario 1: Angle CBD within a Triangle
If angle CBD is part of a triangle, we can utilize several key theorems:
- Angle Sum Theorem: The sum of the measures of the three angles in any triangle is always 180 degrees. If you know the measures of two angles in the triangle containing angle CBD, you can easily find the measure of angle CBD by subtracting the sum of the other two angles from 180 degrees.
Example: In triangle ABC, angle A = 60 degrees, angle B = 70 degrees. Angle C (which might be angle CBD) would be 180 - (60 + 70) = 50 degrees.
-
Isosceles Triangle Theorem: If two sides of a triangle are congruent (equal in length), then the angles opposite those sides are also congruent. This theorem can be useful if you know the triangle is isosceles and the measure of one of the base angles.
-
Equilateral Triangle Theorem: In an equilateral triangle (all three sides are equal), all three angles are congruent and each measures 60 degrees.
Scenario 2: Angle CBD within a Quadrilateral
If angle CBD is part of a quadrilateral, we can employ different strategies:
-
Quadrilateral Angle Sum Theorem: The sum of the measures of the four angles in any quadrilateral is always 360 degrees. Similar to triangles, knowing three angles allows you to calculate the fourth.
-
Special Quadrilaterals: If the quadrilateral is a special type, such as a rectangle, square, parallelogram, rhombus, or trapezoid, additional properties apply. For example, in a rectangle, all angles are right angles (90 degrees). In a parallelogram, opposite angles are congruent. These properties significantly simplify the process of finding angle measures.
Scenario 3: Angle CBD formed by Intersecting Lines
If angle CBD is formed by intersecting lines, the concept of vertical angles and supplementary angles becomes crucial:
-
Vertical Angles Theorem: As mentioned earlier, vertical angles are congruent. If you know the measure of one vertical angle to angle CBD, you automatically know the measure of angle CBD.
-
Supplementary Angles Theorem: If angle CBD is adjacent to another angle and they form a straight line (180 degrees), you can find the measure of angle CBD by subtracting the measure of the adjacent angle from 180 degrees.
Scenario 4: Angle CBD and Trigonometry
In more advanced scenarios, trigonometry can be employed to determine angle CBD. This usually involves using trigonometric functions (sine, cosine, tangent) and known side lengths within a right-angled triangle that includes angle CBD. This method requires a good understanding of trigonometric ratios and the Pythagorean theorem.
Problem-Solving Strategies and Examples
Let's illustrate these concepts with some examples:
Example 1: Triangle ABC
Given: Triangle ABC, angle A = 50 degrees, angle B = 60 degrees. Find angle C (assuming angle C is angle CBD).
Solution: Using the Angle Sum Theorem, angle C = 180 - (50 + 60) = 70 degrees. Therefore, the measure of angle CBD is 70 degrees.
Example 2: Quadrilateral ABCD
Given: Quadrilateral ABCD, angle A = 80 degrees, angle B = 100 degrees, angle C = 110 degrees. Find angle D (assuming angle D is angle CBD).
Solution: Using the Quadrilateral Angle Sum Theorem, angle D = 360 - (80 + 100 + 110) = 70 degrees. Therefore, the measure of angle CBD is 70 degrees.
Example 3: Intersecting Lines
Given: Two intersecting lines forming angles a, b, c, and d. Angle a = 110 degrees. Angle c is vertically opposite to angle a. Find the measure of angle c (assuming angle c is angle CBD).
Solution: Since angles a and c are vertical angles, they are congruent. Therefore, the measure of angle CBD (angle c) is 110 degrees.
Example 4: Using Trigonometry
Imagine a right-angled triangle where angle CBD is one of the acute angles. If the lengths of the side opposite angle CBD (let's call it 'opposite') and the side adjacent to angle CBD (let's call it 'adjacent') are known, we can use the tangent function:
tan(CBD) = opposite / adjacent
By calculating the inverse tangent (arctan) of the ratio, we can find the measure of angle CBD.
Conclusion: Mastering Angle Measurement
Determining the measure of angle CBD, or any angle for that matter, is a fundamental skill in geometry. By understanding the various theorems, postulates, and problem-solving strategies outlined in this guide, you will be well-equipped to tackle a broad range of angle measurement problems. Remember to carefully analyze the given information, identify the relevant geometric principles, and apply the appropriate methods to arrive at the correct solution. Consistent practice and a firm grasp of fundamental concepts will solidify your understanding and build your confidence in solving geometric problems. The more you practice, the more intuitive and efficient your problem-solving process will become. Remember to always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
Which Of The Following Is A Non Renewable Source Of Energy
Apr 04, 2025
-
What Binds To The Exposed Cross Bridges On Actin
Apr 04, 2025
-
All Squares Are Rectangles And Rhombuses
Apr 04, 2025
-
What Is The Role Of Toothpaste In Preventing Cavities
Apr 04, 2025
-
Is A Grasshopper A Producer Consumer Or Decomposer
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Measure Of Angle Cbd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
