What Is The Equivalent Capacitance Of The Four Capacitors
News Leon
Apr 03, 2025 · 6 min read
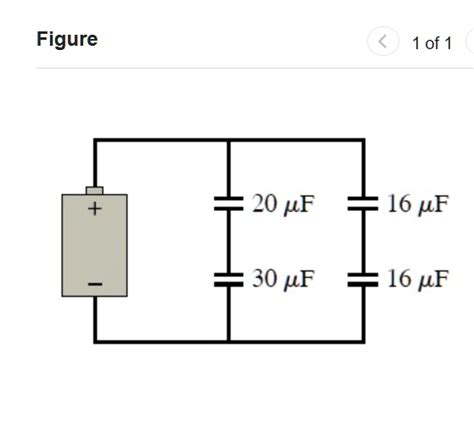
Table of Contents
What is the Equivalent Capacitance of Four Capacitors? A Comprehensive Guide
Understanding how to calculate the equivalent capacitance of multiple capacitors is crucial in electronics and circuit design. This comprehensive guide delves into the methods for determining the equivalent capacitance when dealing with four capacitors, covering various configurations and providing practical examples. We'll explore both series and parallel connections, as well as more complex combinations. By the end, you'll have a solid grasp of this fundamental concept.
Understanding Capacitance
Before diving into calculations, let's refresh our understanding of capacitance. Capacitance (C) is the ability of a capacitor to store electrical energy in an electric field. It's measured in Farads (F), although microfarads (µF), nanofarads (nF), and picofarads (pF) are more commonly used in practice. A capacitor consists of two conductive plates separated by an insulating material called a dielectric. The capacitance value depends on the area of the plates, the distance between them, and the dielectric constant of the insulating material. The greater the area, the higher the capacitance; the smaller the distance, the higher the capacitance; and the higher the dielectric constant, the higher the capacitance.
Capacitor Formulas: A Quick Recap
-
Capacitance (C): This represents the ability of a capacitor to store charge. The basic formula isn't always directly applicable when dealing with multiple capacitors.
-
Charge (Q): This represents the amount of electrical charge stored on the capacitor's plates. The relationship between charge, capacitance, and voltage (V) is given by:
Q = CV -
Energy (E): This represents the energy stored in the capacitor's electric field. The formula for energy stored is:
E = 1/2 * CV²
Equivalent Capacitance: Series Connections
When capacitors are connected in series, the total equivalent capacitance (C<sub>eq</sub>) is always less than the smallest individual capacitance. This is because the total voltage across the series combination is the sum of the voltages across each capacitor, while the charge on each capacitor is the same.
The formula for calculating the equivalent capacitance of capacitors connected in series is:
1/C<sub>eq</sub> = 1/C₁ + 1/C₂ + 1/C₃ + 1/C₄
Example 1: Four Capacitors in Series
Let's say we have four capacitors with the following capacitances:
- C₁ = 10 µF
- C₂ = 20 µF
- C₃ = 30 µF
- C₄ = 40 µF
To find the equivalent capacitance:
-
Calculate the reciprocal of each capacitance:
- 1/C₁ = 0.1
- 1/C₂ = 0.05
- 1/C₃ = 0.0333
- 1/C₄ = 0.025
-
Sum the reciprocals:
- 1/C<sub>eq</sub> = 0.1 + 0.05 + 0.0333 + 0.025 = 0.2083
-
Find the reciprocal of the sum to get the equivalent capacitance:
- C<sub>eq</sub> = 1 / 0.2083 ≈ 4.8 µF
Therefore, the equivalent capacitance of these four capacitors in series is approximately 4.8 µF. Notice that this is significantly less than the smallest individual capacitance (10 µF).
Equivalent Capacitance: Parallel Connections
When capacitors are connected in parallel, the total equivalent capacitance (C<sub>eq</sub>) is simply the sum of the individual capacitances. This is because the voltage across each capacitor is the same, while the total charge is the sum of the charges on each capacitor.
The formula for calculating the equivalent capacitance of capacitors connected in parallel is:
C<sub>eq</sub> = C₁ + C₂ + C₃ + C₄
Example 2: Four Capacitors in Parallel
Using the same capacitors as in Example 1:
- C₁ = 10 µF
- C₂ = 20 µF
- C₃ = 30 µF
- C₄ = 40 µF
The equivalent capacitance is:
C<sub>eq</sub> = 10 µF + 20 µF + 30 µF + 40 µF = 100 µF
The equivalent capacitance of these four capacitors in parallel is 100 µF. This is significantly greater than the largest individual capacitance (40 µF).
More Complex Configurations: Series-Parallel Combinations
Many circuits involve more complex arrangements where capacitors are connected in a combination of series and parallel configurations. To solve these problems, you need to break down the circuit into smaller, simpler parts.
Step-by-step approach:
-
Identify parallel groups: First, look for groups of capacitors connected in parallel. Calculate the equivalent capacitance for each parallel group using the formula
C<sub>eq</sub> = C₁ + C₂ + .... -
Reduce to series: Replace each parallel group with its equivalent capacitance. Then, calculate the equivalent capacitance for the resulting series connection using the formula
1/C<sub>eq</sub> = 1/C₁ + 1/C₂ + .... -
Repeat as necessary: If the circuit is still complex, repeat steps 1 and 2 until you have a single equivalent capacitance.
Example 3: A Series-Parallel Combination
Imagine a circuit with three capacitors:
- C₁ and C₂ are in parallel.
- C₃ is in series with the equivalent capacitance of C₁ and C₂.
Let's assume:
- C₁ = 5 µF
- C₂ = 15 µF
- C₃ = 10 µF
-
Parallel combination of C₁ and C₂:
C<sub>eq(1,2)</sub> = C₁ + C₂ = 5 µF + 15 µF = 20 µF -
Series combination of C<sub>eq(1,2)</sub> and C₃:
1/C<sub>eq</sub> = 1/C<sub>eq(1,2)</sub> + 1/C₃ = 1/20 µF + 1/10 µF = 0.05 + 0.1 = 0.15C<sub>eq</sub> = 1 / 0.15 ≈ 6.67 µF
Therefore, the equivalent capacitance of this series-parallel combination is approximately 6.67 µF.
Practical Applications and Considerations
Understanding equivalent capacitance is vital in various electronic applications:
-
Filter design: Capacitors are frequently used in filters to block certain frequencies while allowing others to pass. The equivalent capacitance determines the filter's cutoff frequency.
-
Power supplies: Capacitors are crucial in smoothing the output voltage of power supplies. The equivalent capacitance affects the ripple voltage.
-
Timing circuits: Capacitors are used in timing circuits to control the duration of pulses or oscillations. The equivalent capacitance affects the timing.
-
Energy storage: In some applications, multiple capacitors might be used in parallel to increase the total energy storage capacity.
Important Considerations:
-
Tolerance: Capacitors have a tolerance that indicates the range of possible values. When calculating equivalent capacitance, keep in mind that the final value might deviate slightly from the calculated value due to the tolerances of the individual capacitors.
-
Voltage ratings: When combining capacitors, ensure that the voltage rating of the equivalent capacitance is sufficient to handle the voltage across the combination. In series connections, the voltage across each capacitor might be higher than the total voltage across the combination.
-
Temperature effects: The capacitance of capacitors can change with temperature. This effect might need to be considered in applications with significant temperature variations.
Conclusion
Calculating the equivalent capacitance of multiple capacitors is a fundamental skill for anyone working with electronic circuits. This guide has covered series, parallel, and series-parallel combinations, providing step-by-step examples and practical considerations. By understanding these concepts, you'll be better equipped to design, analyze, and troubleshoot electronic circuits involving multiple capacitors. Remember to always carefully consider the individual capacitance values, the circuit configuration, and the practical limitations of the components involved. Mastering this skill is essential for success in electronics and circuit design.
Latest Posts
Latest Posts
-
Which Of The Following Reactions Is A Double Displacement Reaction
Apr 04, 2025
-
A Square Is Inscribed In A Right Triangle
Apr 04, 2025
-
A Demand Curve Slopes Downward Because
Apr 04, 2025
-
Lines Ab And Cd Are Parallel
Apr 04, 2025
-
Oxidation Number Of Cl In Clo3
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Equivalent Capacitance Of The Four Capacitors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
