Lines Ab And Cd Are Parallel
News Leon
Apr 04, 2025 · 7 min read
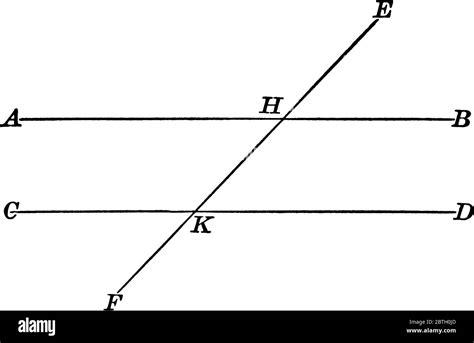
Table of Contents
- Lines Ab And Cd Are Parallel
- Table of Contents
- Lines AB and CD are Parallel: A Comprehensive Exploration of Geometry
- Defining Parallel Lines
- Transversals and their Impact on Parallel Lines
- Types of Angles Formed by a Transversal
- Theorems and Postulates Related to Parallel Lines
- Applications of Parallel Lines
- Architecture and Construction
- Engineering
- Computer Graphics and CAD
- Cartography and Mapping
- Art and Design
- Solving Problems Involving Parallel Lines
- Beyond the Basics: Extending the Understanding of Parallel Lines
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Lines AB and CD are Parallel: A Comprehensive Exploration of Geometry
When two lines, AB and CD, are parallel, a whole world of geometrical relationships opens up. Understanding these relationships is fundamental to geometry, and crucial for success in fields like architecture, engineering, and computer graphics. This article delves deep into the properties and implications of parallel lines, examining various theorems, postulates, and applications. We'll explore how parallel lines interact with transversals, leading to angle relationships that are both predictable and powerfully useful.
Defining Parallel Lines
Parallel lines are lines in a plane that never intersect, no matter how far they are extended. This seemingly simple definition holds the key to understanding a vast array of geometric principles. The notation used to indicate parallel lines is two parallel vertical lines, for example, AB || CD signifies that line AB is parallel to line CD.
Think of train tracks; they are designed to be parallel lines, ensuring that the trains remain on their designated paths. Similarly, the lines on a ruled notebook are parallel, offering a structured framework for writing. These everyday examples highlight the practical significance of parallel lines.
Transversals and their Impact on Parallel Lines
A transversal is a line that intersects two or more other lines. When a transversal intersects two parallel lines, a series of angle relationships are formed. These relationships are crucial for solving geometric problems and are consistent regardless of the specific orientation of the lines.
Let's consider a transversal line 't' intersecting parallel lines AB and CD. This intersection creates eight angles. These angles can be classified into various types:
Types of Angles Formed by a Transversal
-
Interior Angles: These angles are located between the parallel lines. There are four interior angles: angles 3, 4, 5, and 6.
-
Exterior Angles: These angles are located outside the parallel lines. There are four exterior angles: angles 1, 2, 7, and 8.
-
Consecutive Interior Angles: These are pairs of interior angles that are on the same side of the transversal. Examples include angles 3 and 5, and angles 4 and 6. Consecutive interior angles are supplementary, meaning their sum is 180°.
-
Alternate Interior Angles: These are pairs of interior angles that are on opposite sides of the transversal. Examples include angles 3 and 6, and angles 4 and 5. Alternate interior angles are congruent, meaning they have the same measure.
-
Alternate Exterior Angles: These are pairs of exterior angles that are on opposite sides of the transversal. Examples include angles 1 and 8, and angles 2 and 7. Alternate exterior angles are congruent.
-
Corresponding Angles: These are pairs of angles, one interior and one exterior, that are on the same side of the transversal and in corresponding positions relative to the parallel lines. Examples include angles 1 and 5, angles 2 and 6, angles 3 and 7, and angles 4 and 8. Corresponding angles are congruent.
Theorems and Postulates Related to Parallel Lines
The relationships described above are not arbitrary; they are based on fundamental geometric theorems and postulates. These provide the logical framework for understanding why these angle relationships exist.
-
Parallel Postulate (Euclid's Fifth Postulate): This states that through a point not on a given line, there is exactly one line parallel to the given line. This postulate forms the cornerstone of Euclidean geometry.
-
Converse of the Alternate Interior Angles Theorem: If two lines are intersected by a transversal and the alternate interior angles are congruent, then the lines are parallel.
-
Converse of the Corresponding Angles Theorem: If two lines are intersected by a transversal and the corresponding angles are congruent, then the lines are parallel.
-
Converse of the Consecutive Interior Angles Theorem: If two lines are intersected by a transversal and the consecutive interior angles are supplementary, then the lines are parallel.
These theorems allow us to deduce the parallelism of lines based on the angles formed by a transversal. They are instrumental in proving other geometric relationships and solving problems.
Applications of Parallel Lines
The concept of parallel lines extends far beyond theoretical geometry. It finds practical applications in numerous fields:
Architecture and Construction
Parallel lines are fundamental to architectural design and construction. The parallel alignment of walls, beams, and columns ensures structural stability and aesthetic balance. Understanding parallel lines is crucial for accurate measurements, blueprint interpretation, and construction efficiency.
Engineering
Engineers utilize parallel lines in various aspects of their work. From designing bridges and roadways to creating mechanical systems, the concept of parallel lines ensures proper functionality and safety. Precise alignment and parallelism are critical for the smooth operation of machinery and infrastructure.
Computer Graphics and CAD
Computer-aided design (CAD) software relies heavily on the concept of parallel lines. Creating precise drawings, models, and simulations requires accurate representation of parallel lines and their relationships. These tools are essential in various industries, including architecture, engineering, manufacturing, and gaming.
Cartography and Mapping
Parallel lines are used in map projections, especially in grid systems like latitude and longitude. The meridians (lines of longitude) are nearly parallel, providing a framework for accurately representing locations on a map. Understanding the parallelism of these lines is essential for navigation and geographic information systems (GIS).
Art and Design
Parallel lines are often employed in art and design to create visual balance, perspective, and depth. Artists utilize parallel lines to create illusions of distance, structure, and movement. The parallel lines in a painting can contribute significantly to the overall composition and aesthetic appeal.
Solving Problems Involving Parallel Lines
Numerous problems can be solved using the properties of parallel lines and their relationship with transversals. Here's a sample problem:
Problem: Two parallel lines are intersected by a transversal. One of the alternate interior angles measures 75°. Find the measure of the other alternate interior angle and the other three interior angles.
Solution:
-
Alternate Interior Angles: Since the lines are parallel, the alternate interior angles are congruent. Therefore, the other alternate interior angle also measures 75°.
-
Consecutive Interior Angles: Consecutive interior angles are supplementary. Let's consider the pair of consecutive interior angles that includes the 75° angle. The sum of these angles is 180°. Therefore, the other consecutive interior angle measures 180° - 75° = 105°.
-
Remaining Interior Angles: The other two interior angles are alternate interior angles to each other, so they are congruent. Furthermore, they are consecutive interior angles to the 105° angle we calculated earlier. Therefore, each of these remaining angles also measures 105°.
This is a simple example, but the principles remain the same for more complex scenarios. The key is to identify the angle relationships (alternate interior, corresponding, consecutive interior) and use the theorems related to parallel lines to find the unknown angle measures.
Beyond the Basics: Extending the Understanding of Parallel Lines
While this article has focused on the fundamental properties of parallel lines, the concept extends into more advanced geometrical concepts. For instance, the concept of parallelism plays a critical role in:
-
Projective Geometry: Here, parallel lines are considered to intersect at a "point at infinity." This seemingly paradoxical concept expands the realm of geometric transformations and analysis.
-
Non-Euclidean Geometries: In geometries like hyperbolic geometry, the parallel postulate is modified, leading to different properties of lines and their relationships.
-
Vector Geometry: The concept of parallel vectors directly relates to the parallelism of lines, offering an algebraic framework for understanding and manipulating parallel lines.
Conclusion
The concept of parallel lines, while seemingly simple, forms the bedrock of many geometrical principles and finds widespread applications in various fields. Understanding the relationships between parallel lines and transversals, along with related theorems and postulates, is essential for solving geometric problems and applying geometric principles to real-world scenarios. From architecture and engineering to computer graphics and art, the significance of parallel lines is undeniable, highlighting their enduring importance in mathematics and beyond. Continued exploration of these concepts can lead to a deeper appreciation of geometry and its vast applications.
Latest Posts
Latest Posts
-
Are Ribosomes Found In Both Prokaryotic And Eukaryotic Cells
Apr 06, 2025
-
Did The King Change His Mind
Apr 06, 2025
-
How Does Ka Relate To Acid Strength
Apr 06, 2025
-
Which Molecule Has A Higher Potential Energy
Apr 06, 2025
-
Is Energy Recycled In The Ecosystem
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Lines Ab And Cd Are Parallel . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
