How Many Orbitals Are There In The 3d Subshell
News Leon
Apr 06, 2025 · 6 min read
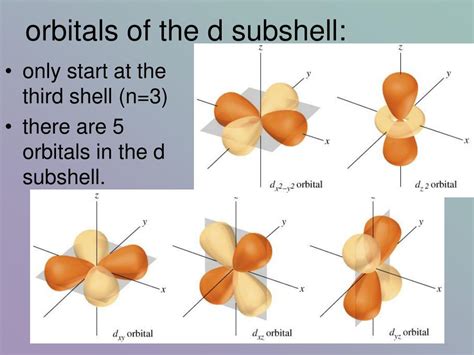
Table of Contents
How Many Orbitals Are There in the 3d Subshell? A Deep Dive into Atomic Structure
Understanding atomic structure is fundamental to grasping the behavior of matter. A key element of this understanding involves comprehending electron configurations and the spatial distribution of electrons within atoms. This article delves into the specifics of the 3d subshell, addressing the central question: How many orbitals are there in the 3d subshell? We will explore the underlying principles of quantum mechanics that dictate the number of orbitals and their shapes, providing a comprehensive overview suitable for students and enthusiasts alike.
Quantum Numbers: The Key to Understanding Atomic Structure
Before we answer the main question, let's review the fundamental quantum numbers that define the properties of atomic orbitals. These numbers provide a mathematical description of the electron's state within an atom:
-
Principal Quantum Number (n): This number describes the energy level of the electron and the size of the orbital. It can take on positive integer values (n = 1, 2, 3...). Higher values of 'n' indicate higher energy levels and larger orbitals. For the 3d subshell, n = 3.
-
Azimuthal Quantum Number (l): This number defines the shape of the orbital and the subshell. It can take integer values from 0 to n-1. For a given value of 'n', there are 'n' possible values of 'l'. Specific values of 'l' correspond to different subshells:
- l = 0: s subshell (spherical)
- l = 1: p subshell (dumbbell-shaped)
- l = 2: d subshell (more complex shapes)
- l = 3: f subshell (even more complex shapes)
For the 3d subshell, n = 3, so the possible values of 'l' are 0, 1, and 2. The 3d subshell corresponds to l = 2.
-
Magnetic Quantum Number (ml): This number specifies the orientation of the orbital in space. It can take integer values from -l to +l, including 0. This means there are 2l + 1 possible orientations for a given subshell.
-
Spin Quantum Number (ms): This number describes the intrinsic angular momentum (spin) of the electron. It can only have two values: +1/2 (spin up) or -1/2 (spin down). This is independent of the other three quantum numbers.
Determining the Number of Orbitals in the 3d Subshell
Now, let's apply these quantum numbers to determine the number of orbitals in the 3d subshell. We know that for the 3d subshell:
- n = 3
- l = 2
The magnetic quantum number (ml) can take values from -l to +l, so for l = 2, the possible values of ml are: -2, -1, 0, +1, +2.
This gives us five possible values for ml. Each unique combination of n, l, and ml represents a different atomic orbital. Therefore, there are five 3d orbitals.
The Shapes of the 3d Orbitals
The five 3d orbitals have distinct shapes, although they all possess the same energy level within the 3d subshell (except in the presence of ligand fields in coordination complexes). These shapes are more complex than the s and p orbitals:
-
d<sub>xy</sub>: This orbital has four lobes, with electron density concentrated along the x and y axes.
-
d<sub>xz</sub>: Similar to d<sub>xy</sub>, this orbital has four lobes, but the electron density is concentrated along the x and z axes.
-
d<sub>yz</sub>: This orbital also has four lobes, with electron density concentrated along the y and z axes.
-
d<sub>x² - y²</sub>: This orbital has four lobes, with electron density concentrated along the x and y axes, but with a nodal plane bisecting the axes.
-
d<sub>z²</sub>: This orbital has a unique shape with two lobes along the z-axis and a donut-shaped region in the xy plane.
Visual representations of these orbitals are readily available online and in chemistry textbooks. Understanding these shapes helps in visualizing the spatial distribution of electrons within the atom and contributes to a deeper understanding of chemical bonding and molecular geometry.
Significance of the 3d Orbitals in Chemistry
The 3d orbitals play a crucial role in the chemistry of transition metals. These metals have partially filled 3d subshells, leading to their characteristic properties such as variable oxidation states, catalytic activity, and vibrant colors in their compounds. The involvement of 3d orbitals in bonding and electronic transitions explains many observations in transition metal chemistry.
For instance, the formation of coordination complexes with transition metals involves the interaction between the metal's 3d orbitals and ligands. The specific geometry and properties of these complexes are directly related to the number and orientation of the 3d orbitals.
Moreover, the electronic transitions between the 3d orbitals are responsible for the absorption of light in many transition metal complexes, resulting in the characteristic colors of these compounds. This principle is fundamental in spectrophotometry and colorimetric analysis.
Beyond the 3d Subshell: Expanding on Quantum Mechanics
The principles governing the 3d subshell apply equally to other subshells. The number of orbitals in a subshell is always 2l + 1, where 'l' is the azimuthal quantum number. This allows us to determine the number of orbitals in any subshell:
- s subshell (l = 0): 2(0) + 1 = 1 orbital
- p subshell (l = 1): 2(1) + 1 = 3 orbitals
- d subshell (l = 2): 2(2) + 1 = 5 orbitals
- f subshell (l = 3): 2(3) + 1 = 7 orbitals And so on.
This systematic approach, rooted in quantum mechanics, provides a powerful framework for understanding the electronic structure of atoms and molecules, forming the bedrock of much of modern chemistry and physics.
Addressing Common Misconceptions
A common misconception is confusing the number of orbitals with the number of electrons a subshell can hold. While the 3d subshell has five orbitals, each orbital can hold a maximum of two electrons (due to the Pauli Exclusion Principle). Therefore, the 3d subshell can hold a total of 10 electrons. It's crucial to distinguish between the number of orbitals and the maximum electron capacity.
Conclusion: A Recap on the 3d Subshell
In conclusion, the 3d subshell contains five orbitals. This number is determined by the azimuthal quantum number (l = 2) and the magnetic quantum number (ml), which can take five distinct values (-2, -1, 0, 1, 2). Each of these orbitals has a specific shape and orientation in space, and their involvement in chemical bonding and electronic transitions is crucial in understanding the properties of transition metals and their compounds. The concepts of quantum numbers and their implications form the cornerstone of understanding atomic structure and chemical behavior. A thorough grasp of this fundamental aspect is essential for further exploration in the realms of chemistry and physics.
Latest Posts
Latest Posts
-
Definition Of Initial Velocity In Physics
Apr 06, 2025
-
Which Of The Following Is True Of Annuities
Apr 06, 2025
-
How Much Is 20 Of 500
Apr 06, 2025
-
Calcium Carbonate And Hydrochloric Acid Balanced Equation
Apr 06, 2025
-
Face Centered Cubic Unit Cell Coordination Number
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Many Orbitals Are There In The 3d Subshell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
