Greatest Common Factor Of 54 And 36
News Leon
Mar 29, 2025 · 5 min read
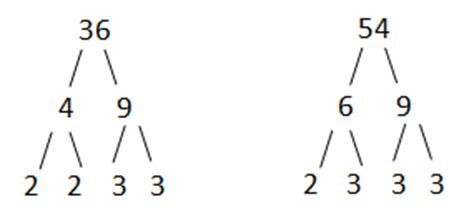
Table of Contents
Finding the Greatest Common Factor (GCF) of 54 and 36: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with applications spanning various fields, from simplifying fractions to solving algebraic equations. This comprehensive guide will delve deep into the methods for determining the GCF of 54 and 36, exploring different approaches and illustrating the underlying principles. We'll also look at the broader applications of finding the GCF and how it relates to other mathematical concepts.
Understanding the Greatest Common Factor (GCF)
Before we jump into finding the GCF of 54 and 36, let's establish a clear understanding of what the GCF represents. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that goes into both numbers evenly.
For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The greatest of these common factors is 6, therefore, the GCF of 12 and 18 is 6.
Method 1: Listing Factors
This is the most straightforward method, especially for smaller numbers like 54 and 36. Let's list the factors of each number:
Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Now, identify the common factors: 1, 2, 3, 6, 9, and 18. The greatest of these common factors is 18. Therefore, the GCF(54, 36) = 18.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the underlying mathematical principles. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime Factorization of 54:
54 = 2 x 27 = 2 x 3 x 9 = 2 x 3 x 3 x 3 = 2 x 3³
Prime Factorization of 36:
36 = 2 x 18 = 2 x 2 x 9 = 2 x 2 x 3 x 3 = 2² x 3²
Now, identify the common prime factors and their lowest powers:
- Common prime factor 2: The lowest power is 2¹ (or simply 2).
- Common prime factor 3: The lowest power is 3².
Multiply these common prime factors with their lowest powers together: 2 x 3² = 2 x 9 = 18. Therefore, the GCF(54, 36) = 18.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, which is the GCF.
Let's apply the Euclidean algorithm to 54 and 36:
- Subtract the smaller number from the larger number: 54 - 36 = 18
- Replace the larger number with the result: Now we find the GCF of 36 and 18.
- Repeat the process: 36 - 18 = 18
- The process stops when the two numbers are equal: The GCF is 18.
Therefore, the GCF(54, 36) = 18.
Applications of the Greatest Common Factor
The GCF has numerous applications across various mathematical areas and real-world scenarios:
1. Simplifying Fractions:
The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 54/36 can be simplified by dividing both the numerator and the denominator by their GCF (18): 54/36 = (54 ÷ 18) / (36 ÷ 18) = 3/2.
2. Solving Algebraic Equations:
The GCF plays a vital role in factoring algebraic expressions. For example, when factoring the expression 54x + 36y, we can factor out the GCF (18) to simplify the expression: 18(3x + 2y).
3. Geometry and Measurement:
The GCF is used in solving geometric problems involving area and volume calculations. For instance, if you need to divide a rectangular area of 54 square units into equal smaller squares, the GCF helps determine the side length of the largest possible square.
4. Number Theory:
The GCF is a cornerstone concept in number theory, influencing studies of divisibility, prime numbers, and modular arithmetic.
Understanding the Least Common Multiple (LCM) in Relation to GCF
While we've focused on the GCF, it's important to understand its relationship with the least common multiple (LCM). The LCM of two numbers is the smallest positive integer that is a multiple of both numbers. The GCF and LCM are related through the following formula:
LCM(a, b) x GCF(a, b) = a x b
For 54 and 36:
We know GCF(54, 36) = 18. Using the formula:
LCM(54, 36) x 18 = 54 x 36
LCM(54, 36) = (54 x 36) / 18 = 108
Therefore, the LCM of 54 and 36 is 108. This relationship between GCF and LCM is valuable in various mathematical applications.
Conclusion: Mastering the GCF
Finding the greatest common factor is a fundamental skill in mathematics with wide-ranging applications. We've explored three effective methods for determining the GCF – listing factors, prime factorization, and the Euclidean algorithm – each providing a unique approach to solving the problem. Understanding the GCF not only aids in simplifying calculations but also provides a deeper understanding of number theory and its connections to other mathematical concepts. By mastering these methods, you'll be well-equipped to tackle more complex mathematical challenges and enhance your problem-solving abilities. Remember to choose the method that best suits the numbers you're working with and the level of detail required. Whether you're simplifying fractions, factoring algebraic expressions, or solving geometrical problems, a solid grasp of the GCF is an invaluable asset in your mathematical toolkit. The consistent application of these techniques will lead to improved fluency and a stronger foundation in mathematics.
Latest Posts
Latest Posts
-
Which Of The Following Organisms Has An Open Circulatory System
Apr 01, 2025
-
What Is The Prime Factorization Of 980
Apr 01, 2025
-
Concentration Of Hydrogen Ions In Water With Ph Of 7
Apr 01, 2025
-
An Example Of A Transfer Payment Is
Apr 01, 2025
-
4 Right Angles And 4 Equal Sides
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 54 And 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
