What Is The Prime Factorization Of 980
News Leon
Apr 01, 2025 · 5 min read
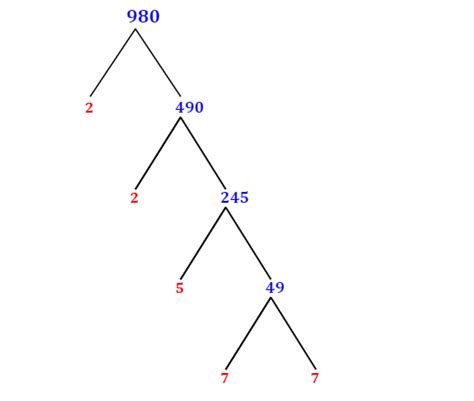
Table of Contents
What is the Prime Factorization of 980? A Deep Dive into Prime Numbers and Factorization
Finding the prime factorization of a number might seem like a simple mathematical exercise, but it's a fundamental concept with far-reaching implications in number theory and cryptography. This article will delve into the prime factorization of 980, explaining the process step-by-step and exploring the broader context of prime numbers and their significance. We'll also touch upon practical applications and related mathematical concepts.
Understanding Prime Numbers
Before we tackle the prime factorization of 980, let's clarify what prime numbers are. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. This means it cannot be expressed as a product of two smaller whole numbers. The first few prime numbers are 2, 3, 5, 7, 11, 13, and so on. The number 1 is not considered a prime number.
The fundamental theorem of arithmetic states that every integer greater than 1 can be represented uniquely as a product of prime numbers, disregarding the order of the factors. This unique representation is known as the prime factorization of the number. This theorem forms the bedrock of many number-theoretic concepts.
Finding the Prime Factorization of 980: A Step-by-Step Approach
To find the prime factorization of 980, we employ a systematic approach, repeatedly dividing by the smallest prime number possible until we are left with only prime numbers.
-
Start with the smallest prime number, 2: 980 is an even number, so it's divisible by 2. 980 ÷ 2 = 490
-
Continue dividing by 2: 490 is also even. 490 ÷ 2 = 245
-
Move to the next prime number, 3: 245 is not divisible by 3 (the sum of its digits, 2 + 4 + 5 = 11, is not divisible by 3).
-
Move to the next prime number, 5: 245 ends in 5, so it's divisible by 5. 245 ÷ 5 = 49
-
Move to the next prime number, 7: 49 is divisible by 7. 49 ÷ 7 = 7
-
We're left with 7: 7 is a prime number.
Therefore, the prime factorization of 980 is 2 x 2 x 5 x 7 x 7, which can also be written as 2² x 5 x 7².
Visualizing Prime Factorization: Factor Trees
A helpful visual aid for finding prime factorization is a factor tree. Here's how to construct one for 980:
980
/ \
2 490
/ \
2 245
/ \
5 49
/ \
7 7
The factor tree systematically breaks down the number until all branches end in prime numbers. The prime factorization is then obtained by multiplying all the prime numbers at the ends of the branches.
Beyond the Basics: Applications and Related Concepts
The seemingly simple process of prime factorization has profound implications in various fields:
1. Cryptography:
Prime numbers are the cornerstone of modern cryptography, particularly in RSA encryption. RSA relies on the difficulty of factoring very large numbers into their prime components. The security of many online transactions hinges on this computational challenge. The larger the numbers involved, the more secure the encryption.
2. Number Theory:
Prime factorization is a fundamental concept in number theory. It's used to solve various problems, including:
- Finding the greatest common divisor (GCD): The GCD of two numbers can be efficiently calculated using their prime factorizations.
- Solving Diophantine equations: These are equations where only integer solutions are sought. Prime factorization often plays a crucial role in solving these types of equations.
- Investigating properties of numbers: Prime factorization helps in understanding the structure and properties of numbers, such as their divisibility and relationships with other numbers.
3. Modular Arithmetic:
Modular arithmetic deals with remainders after division. Prime numbers have special properties in modular arithmetic, making them essential in various algorithms and applications. For instance, prime numbers are crucial in the functioning of hash tables and certain types of error-correcting codes.
4. Computer Science:
Prime factorization is used in various computer science algorithms, including:
- Hashing: Distributing data evenly across a hash table.
- Random Number Generation: Creating sequences of seemingly random numbers.
- Primality Testing: Determining whether a given number is prime or not (efficient primality tests are crucial for cryptography).
Advanced Techniques for Larger Numbers
For smaller numbers like 980, the method of repeated division by prime numbers is straightforward. However, for extremely large numbers, more sophisticated algorithms are necessary. These algorithms include:
- Trial division: Testing divisibility by successively larger prime numbers. While simple, it becomes computationally expensive for very large numbers.
- Pollard's rho algorithm: A probabilistic algorithm that's more efficient than trial division for finding factors of large composite numbers.
- General number field sieve (GNFS): The most efficient known algorithm for factoring very large numbers, used to break RSA encryption with large keys.
Conclusion: The Enduring Importance of Prime Factorization
The prime factorization of 980, while seemingly a basic mathematical exercise, reveals a fundamental concept with far-reaching consequences. Understanding prime factorization is essential for grasping the principles of number theory and its applications in cryptography, computer science, and various other fields. As technology continues to advance, the ability to efficiently factor large numbers remains a critical area of research, with implications for the security of digital systems worldwide. The seemingly simple process of breaking down 980 into its prime components (2² x 5 x 7²) opens the door to a fascinating and complex world of mathematical exploration.
Latest Posts
Latest Posts
-
Which Of The Following Combinations Is Correct
Apr 02, 2025
-
How Do You Find The Boiling Point Of A Solution
Apr 02, 2025
-
Balance Equation Fes2 O2 Fe2o3 So2
Apr 02, 2025
-
Which Is Not A Physical Property
Apr 02, 2025
-
Australia Is The Worlds Leading Producer Of
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about What Is The Prime Factorization Of 980 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
