4 Right Angles And 4 Equal Sides
News Leon
Apr 01, 2025 · 6 min read
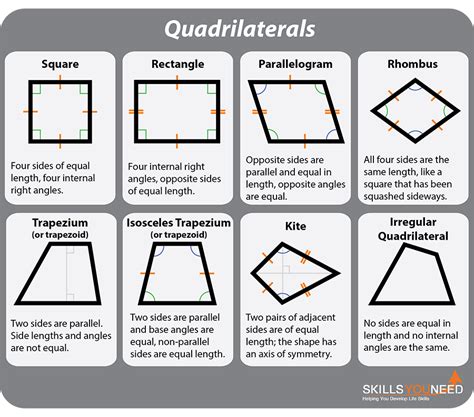
Table of Contents
4 Right Angles and 4 Equal Sides: Exploring the Square
The simple phrase "4 right angles and 4 equal sides" immediately conjures a single, powerful image in the mind of anyone familiar with basic geometry: a square. This seemingly elementary shape, however, holds a significant place in mathematics, art, architecture, and even our everyday lives. This article will delve deep into the fascinating world of squares, exploring their properties, applications, and the mathematical concepts they embody.
Defining the Square: More Than Just Four Sides
A square is a two-dimensional geometric shape defined precisely by its properties: it possesses four sides of equal length and four angles, each measuring 90 degrees (right angles). This seemingly simple definition opens doors to a world of mathematical exploration and practical applications. Understanding the properties of a square allows us to delve into more complex geometric concepts and apply them to various fields.
Key Properties of a Square:
- Equilateral: All four sides are congruent (equal in length). This is a defining characteristic that distinguishes it from other quadrilaterals.
- Equiangular: All four angles are right angles (90°). This property ensures that the opposite sides are parallel to each other.
- Parallel Sides: Opposite sides are parallel. This leads to many useful geometrical properties and theorems.
- Diagonals Bisect Each Other: The diagonals of a square intersect at a point that is exactly halfway along each diagonal. This point is also the center of the square.
- Diagonals are Perpendicular: The diagonals of a square are perpendicular bisectors of each other. This means they intersect at a right angle and divide each other into two equal segments.
- Diagonals Bisect Angles: Each diagonal bisects the angles at the vertices it connects. This means it divides each angle into two equal 45° angles.
The Square in the World of Mathematics:
The square forms the basis for many advanced mathematical concepts. Its inherent symmetry and predictable properties make it a foundational building block in:
1. Euclidean Geometry:
Euclidean geometry, the classical study of shapes and spaces, relies heavily on the square. Theorems related to parallel lines, congruent triangles, and area calculations often utilize squares as examples or components of proofs. The Pythagorean theorem, a cornerstone of Euclidean geometry, directly relates to the sides and diagonal of a square.
2. Coordinate Geometry:
In coordinate geometry, the square provides a simple yet effective framework for understanding coordinates and transformations. Squares defined by coordinates allow for the exploration of rotations, reflections, and translations in a clear and manageable way.
3. Trigonometry:
The 45-45-90 triangle, formed by cutting a square along its diagonal, is a fundamental trigonometric right-angled triangle. The ratios of its sides lead to the understanding of trigonometric functions such as sine, cosine, and tangent at 45 degrees.
4. Calculus:
Even in calculus, squares have their place. For instance, when calculating areas under curves, squares can be used as basic building blocks in approximating integral values using methods like Riemann sums.
Beyond Mathematics: Squares in Art, Architecture, and Design
The square's inherent stability and visual appeal have made it a favorite in various artistic and architectural endeavors throughout history:
1. Art and Design:
From ancient mosaics to modern minimalist art, squares have been a consistent motif. The symmetry and predictability of the square create a sense of balance and order, often used to contrast or complement other shapes. Consider the impact of squares in:
- Tessellations: Squares, being capable of tessellating (fitting together without gaps or overlaps), form the basis for numerous artistic and architectural patterns. Think of tiled floors or intricate mosaics.
- Optical Illusions: The square's properties can be manipulated to create optical illusions, playing with our perception of perspective and dimension.
- Abstract Art: The clean lines and simple form of the square make it a popular element in abstract art, where artists explore concepts of form, space, and color.
2. Architecture and Engineering:
The stability and strength of the square translate directly into its wide use in architecture and engineering:
- Building Construction: Squares and rectangular shapes (which are essentially elongated squares) dominate building construction. They provide structural integrity and facilitate efficient use of space.
- Urban Planning: The grid system used in many cities is based on squares and rectangular blocks, enabling efficient navigation and land division.
- Civil Engineering: Squares appear in structural designs, creating robust and reliable foundations.
Practical Applications of the Square:
Beyond art and architecture, the square finds its way into numerous everyday objects and technologies:
- Packaging: Many products, from boxes to containers, utilize square or rectangular packaging for optimal space utilization and ease of stacking.
- Digital Displays: The square aspect ratio is common in digital displays and screens, impacting screen resolution and image display.
- Games and Puzzles: Squares are fundamental to many games and puzzles, providing a consistent grid for gameplay.
- Textiles: Squares and square patterns are common motifs in textiles, used for creating patterns and designs.
Exploring Variations: The Relationship Between Squares and Other Shapes
While the square is uniquely defined by its properties, it shares relationships with other geometric shapes:
- Rectangle: A rectangle is a quadrilateral with four right angles, but its sides are not necessarily equal. A square is a special type of rectangle where all sides are equal.
- Rhombus: A rhombus is a quadrilateral with four equal sides, but its angles are not necessarily right angles. A square is a special type of rhombus with four right angles.
- Quadrilateral: A square is a specific type of quadrilateral, exhibiting additional properties not shared by all quadrilaterals.
- Polygon: A square is a regular polygon with four sides.
Understanding these relationships helps to grasp the hierarchy and classification within the broader world of geometric shapes.
Advanced Concepts and Further Exploration:
Delving further into the world of squares opens avenues for exploring more complex mathematical and geometrical concepts:
- Higher Dimensions: The concept of a square can be extended to higher dimensions. In three dimensions, we have a cube, which is a three-dimensional analogue of the square. In higher dimensions, we have hypercubes, which are difficult to visualize but are significant in theoretical mathematics.
- Fractal Geometry: Squares can be incorporated into fractal geometry, creating self-similar patterns that repeat at different scales. This leads to fascinating and visually complex structures.
- Geometric Transformations: Exploring transformations such as dilation, rotation, and translation applied to squares enhances the understanding of geometric transformations in general.
- Tessellations and Tilings: The ability of squares to perfectly tessellate is a fascinating topic in its own right. Exploring different tessellations using squares and other shapes introduces mathematical concepts of symmetry and patterns.
Conclusion: The Enduring Significance of the Square
The seemingly simple square, defined by its four equal sides and four right angles, possesses a profound significance in mathematics, art, architecture, and various aspects of our daily lives. Its predictable properties, inherent stability, and visual appeal make it a cornerstone of many fields. From the foundational principles of Euclidean geometry to the intricacies of fractal geometry, the square's influence is pervasive. Its continued importance highlights the power of seemingly simple geometric shapes in shaping our understanding of the world around us. As we continue to explore the complexities of mathematics and the artistry of design, the humble square will undoubtedly remain a significant element in our journey of discovery.
Latest Posts
Latest Posts
-
Which Of The Following Combinations Is Correct
Apr 02, 2025
-
How Do You Find The Boiling Point Of A Solution
Apr 02, 2025
-
Balance Equation Fes2 O2 Fe2o3 So2
Apr 02, 2025
-
Which Is Not A Physical Property
Apr 02, 2025
-
Australia Is The Worlds Leading Producer Of
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 4 Right Angles And 4 Equal Sides . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
