Electric Field Inside A Hollow Sphere
News Leon
Apr 02, 2025 · 6 min read
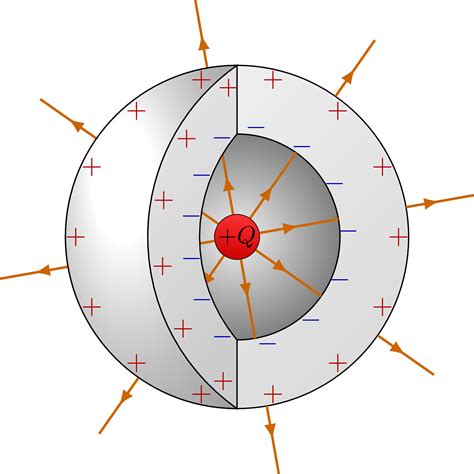
Table of Contents
Electric Field Inside a Hollow Sphere: A Comprehensive Exploration
The concept of the electric field inside a hollow sphere is a cornerstone of electrostatics, offering valuable insights into the behavior of charges and fields. Understanding this seemingly simple scenario requires a solid grasp of Gauss's Law and its implications. This article will delve deep into the subject, explaining the underlying principles, exploring various scenarios, and addressing common misconceptions. We’ll also touch upon the applications of this principle in real-world scenarios.
Understanding Gauss's Law: The Foundation
Before we dive into the specifics of a hollow sphere, it's crucial to understand Gauss's Law, the fundamental theorem that governs this phenomenon. Gauss's Law states that the net electric flux through any closed surface is proportional to the enclosed electric charge. Mathematically, it's expressed as:
∮ E • dA = Q/ε₀
Where:
- ∮ E • dA represents the surface integral of the electric field over the closed surface.
- Q is the total charge enclosed within the surface.
- ε₀ is the electric permittivity of free space (a constant).
This law is incredibly powerful because it allows us to calculate the electric field without having to integrate over individual contributions from each charge. Instead, we can focus on the symmetry of the problem and choose a Gaussian surface that simplifies the calculation.
The Hollow Sphere: A Symmetrical Case
Consider a hollow conducting sphere with a total charge Q distributed uniformly on its outer surface. The key to understanding the electric field inside this sphere lies in the symmetry of the charge distribution and the clever application of Gauss's Law.
Choosing the Gaussian Surface
To apply Gauss's Law, we need to choose a Gaussian surface—an imaginary closed surface—that simplifies the calculation. In this case, we'll choose a spherical Gaussian surface entirely inside the hollow sphere. This surface encloses no charge (since all the charge resides on the outer surface).
Applying Gauss's Law: The Result
Now, let's apply Gauss's Law to our chosen Gaussian surface:
∮ E • dA = Q_enclosed/ε₀
Since the Gaussian surface encloses no charge (Q_enclosed = 0), we have:
∮ E • dA = 0
This equation implies that the electric field E must be zero everywhere inside the hollow sphere. This is a crucial result: The electric field inside a hollow conducting sphere with charge only on its outer surface is zero.
This doesn't just apply to a perfectly uniform charge distribution. As long as the charge is entirely confined to the outer surface, the field inside will be zero, regardless of how it's distributed on that surface. The spherical symmetry of the Gaussian surface and the zero enclosed charge lead inevitably to zero electric field.
Beyond the Conducting Sphere: Non-Conducting Hollow Sphere
The situation changes slightly if we consider a non-conducting hollow sphere with a charge distributed throughout its volume, or on its inner surface. Let's break down different scenarios:
Scenario 1: Charge Distributed Throughout the Volume
If the charge is distributed throughout the volume of a non-conducting hollow sphere, the electric field inside will not be zero. The electric field at any point inside will depend on the charge distribution and will require integration to calculate precisely. The symmetry is less helpful here; we cannot simply use a spherical Gaussian surface and assume a constant electric field.
To calculate the field in this scenario, you would need to use Gauss's Law with a carefully selected Gaussian surface and integrate over the charge distribution within that surface. The complexity depends heavily on the nature of the charge distribution. A uniform charge distribution would be simpler than a non-uniform one.
Scenario 2: Charge on the Inner Surface
If the charge is solely on the inner surface of a non-conducting hollow sphere, the electric field outside the sphere will be zero. However, the electric field inside the sphere will be non-zero. The field will be affected by the distribution of the charge on the inner surface. Once again, to calculate the field you would need to apply Gauss's law using an appropriate Gaussian surface and integrate over the charge on the inner surface.
The same integration method mentioned in Scenario 1 applies here. But unlike the conducting hollow sphere, the field inside a non-conducting one, with charge solely on its inner surface, won't be uniformly zero. The precise field will depend on the spatial distribution of this inner surface charge.
Implications and Applications
The principle of zero electric field inside a hollow conducting sphere has significant implications and applications in various fields:
-
Faraday Cage: This principle is the foundation of a Faraday cage, a conductive enclosure that blocks electromagnetic fields. The zero field inside protects sensitive equipment from external electromagnetic interference. Examples include shielded rooms used in electronics testing or microwave ovens, where the metal casing acts as a Faraday cage to prevent microwave leakage.
-
Electrostatic Shielding: The zero electric field inside a conductor is also exploited in electrostatic shielding. By surrounding sensitive equipment with a conductive material, you can effectively shield it from external electric fields. This is crucial in many applications where precision measurements are required or where equipment needs to be protected from static electricity.
-
Capacitors: The concept is crucial in understanding the behavior of spherical capacitors. The field between the conducting plates of such a capacitor can be analyzed using the concepts outlined above.
-
Fundamental Physics: This seemingly simple concept demonstrates the power of Gauss's Law and highlights the unique behavior of charges within conductors. It is a crucial building block in understanding more advanced concepts in electromagnetism.
Addressing Common Misconceptions
Several common misconceptions surround the electric field inside a hollow sphere:
-
Misconception 1: The electric field is zero only if the charge distribution is perfectly uniform. Reality: The electric field inside a hollow conducting sphere is zero regardless of the charge distribution on its outer surface, due to the charge redistribution on the surface of the conductor. For a non-conducting sphere, this is not the case.
-
Misconception 2: The electric field inside a hollow sphere is always zero. Reality: This is only true for a hollow conducting sphere with charge only on the outer surface. If the charge is inside the sphere (either distributed in the volume or on the inner surface of a non-conducting sphere), the electric field will be non-zero.
-
Misconception 3: Gauss's Law only works for perfectly symmetrical systems. Reality: While symmetry simplifies the application of Gauss's Law, it's a powerful tool that can be applied to any closed surface, regardless of symmetry. The difficulty comes in the mathematical integration, which can be significantly more challenging in systems lacking symmetry.
Conclusion
The electric field inside a hollow sphere provides a fascinating case study in electrostatics. Understanding this principle, which is fundamentally linked to Gauss's Law and the behavior of conductors, is essential for grasping more complex concepts in electromagnetism. Remember, the zero-field condition inside a conducting hollow sphere with charge solely on its outer surface is a powerful and practical concept with many real-world applications, from shielding electronics to understanding the behavior of capacitors. The variations of charge distribution within non-conducting hollow spheres require further calculation and highlight the importance of understanding the specific nature of the charge arrangement to predict the resultant electric field.
Latest Posts
Latest Posts
-
Which Of The Following Graphs Represents A One To One Function
Apr 03, 2025
-
Is B2 2 Paramagnetic Or Diamagnetic
Apr 03, 2025
-
Capital Of Karnataka State In India
Apr 03, 2025
-
Which Of The Following Substances Should Not Be Filtered
Apr 03, 2025
-
What Type Of Bond Links Amino Acids Together
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Inside A Hollow Sphere . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
