Which Of The Following Graphs Represents A One-to-one Function
News Leon
Apr 03, 2025 · 5 min read
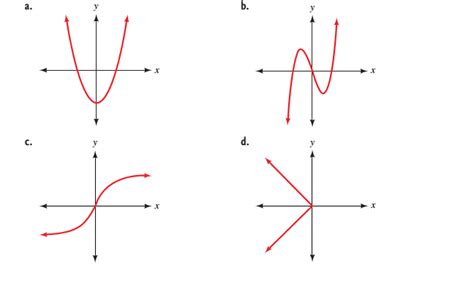
Table of Contents
Which of the Following Graphs Represents a One-to-One Function? A Comprehensive Guide
Understanding functions, particularly one-to-one functions, is crucial in various fields, from mathematics and computer science to engineering and economics. This comprehensive guide will explore the concept of one-to-one functions, explain how to identify them from their graphs, and provide you with a robust methodology to analyze different graphical representations. We'll delve into practical examples and address common misconceptions. By the end, you'll be confident in determining whether a given graph depicts a one-to-one function.
What is a One-to-One Function?
A one-to-one function, also known as an injective function, is a function where each element in the range (output) corresponds to exactly one element in the domain (input). In simpler terms, no two different inputs produce the same output. This contrasts with many-to-one functions, where multiple inputs can map to the same output.
Key Characteristics of a One-to-One Function:
- Unique Output: Each input value produces a unique output value.
- Horizontal Line Test: A crucial graphical test to identify one-to-one functions. If any horizontal line intersects the graph at more than one point, the function is not one-to-one.
- Injective Mapping: A formal mathematical term emphasizing the unique mapping between domain and range elements.
Identifying One-to-One Functions from Graphs: The Horizontal Line Test
The horizontal line test is the most efficient way to determine if a graph represents a one-to-one function. It's a visual approach that allows for quick identification without complex calculations.
How to apply the Horizontal Line Test:
- Draw Horizontal Lines: Imagine drawing several horizontal lines across the entire range of the graph.
- Intersection Points: Observe the number of intersections each horizontal line makes with the graph.
- One-to-One Condition: If every horizontal line intersects the graph at most once, the function is one-to-one. If any horizontal line intersects the graph more than once, the function is not one-to-one.
Examples: Analyzing Graphs for One-to-One Functions
Let's analyze several graphical representations to illustrate the application of the horizontal line test and solidify your understanding.
Example 1: A Straight Line (y = x)
The graph of y = x is a straight line passing through the origin with a slope of 1. Applying the horizontal line test, we see that every horizontal line intersects the graph at exactly one point. Therefore, y = x is a one-to-one function.
Example 2: A Parabola (y = x²)
The graph of y = x² is a parabola opening upwards. If we draw a horizontal line above the x-axis, it will intersect the parabola at two points. This violates the one-to-one condition. Therefore, y = x² is not a one-to-one function.
Example 3: A Cubic Function (y = x³)
The graph of y = x³ is a smoothly increasing curve. Applying the horizontal line test, we find that each horizontal line intersects the graph at only one point. Thus, y = x³ is a one-to-one function.
Example 4: A Trigonometric Function (y = sin x)
The graph of y = sin x is a periodic wave. Many horizontal lines will intersect the graph at infinitely many points. This clearly shows that y = sin x is not a one-to-one function over its entire domain. However, by restricting the domain (for example, to [-π/2, π/2]), we can obtain a one-to-one function (arcsin x). This highlights the importance of considering the domain when analyzing functions.
Example 5: A Piecewise Function
Piecewise functions can be more challenging. Consider a function defined as:
f(x) = x, if x < 0
x², if x ≥ 0
This function's graph consists of a straight line for x < 0 and a parabola for x ≥ 0. A horizontal line above the x-axis will intersect the parabola at two points, while a horizontal line below the x-axis intersects only the straight line at one point. Since some horizontal lines intersect at more than one point, this piecewise function is not one-to-one.
Common Mistakes and Misconceptions
- Confusing One-to-One with Increasing/Decreasing Functions: While many one-to-one functions are either strictly increasing or strictly decreasing, this is not always the case. A function can be one-to-one without being strictly monotonic.
- Ignoring the Domain: The domain of the function plays a crucial role. A function might not be one-to-one over its entire natural domain, but it might be one-to-one when its domain is restricted.
- Misinterpreting the Vertical Line Test: The vertical line test determines if a graph represents a function (whether each input maps to only one output), not whether it's a one-to-one function.
Advanced Considerations and Applications
- Inverse Functions: Only one-to-one functions have inverse functions. The inverse function essentially "reverses" the mapping of the original function.
- Cryptography: One-to-one functions are fundamental in cryptography, ensuring that each encrypted message corresponds to a unique decrypted message.
- Calculus: The concept of injectivity is used in many advanced calculus topics like the inverse function theorem.
Conclusion: Mastering the Identification of One-to-One Functions
Determining whether a graph represents a one-to-one function is a critical skill in mathematics and related fields. By mastering the horizontal line test and understanding the underlying concepts, you can confidently analyze various graphical representations and identify one-to-one functions. Remember to consider the domain and be aware of common misconceptions. With practice, this skill will become second nature, enabling you to tackle more complex mathematical and real-world problems involving functions. The ability to confidently and accurately identify one-to-one functions is a cornerstone of mathematical fluency. Remember, consistent practice and attention to detail will solidify your understanding and lead to effortless application of this essential concept.
Latest Posts
Latest Posts
-
What Binds To The Exposed Cross Bridges On Actin
Apr 04, 2025
-
All Squares Are Rectangles And Rhombuses
Apr 04, 2025
-
What Is The Role Of Toothpaste In Preventing Cavities
Apr 04, 2025
-
Is A Grasshopper A Producer Consumer Or Decomposer
Apr 04, 2025
-
Ac And Bd Bisect Each Other
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Graphs Represents A One-to-one Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
