Ac And Bd Bisect Each Other
News Leon
Apr 04, 2025 · 5 min read
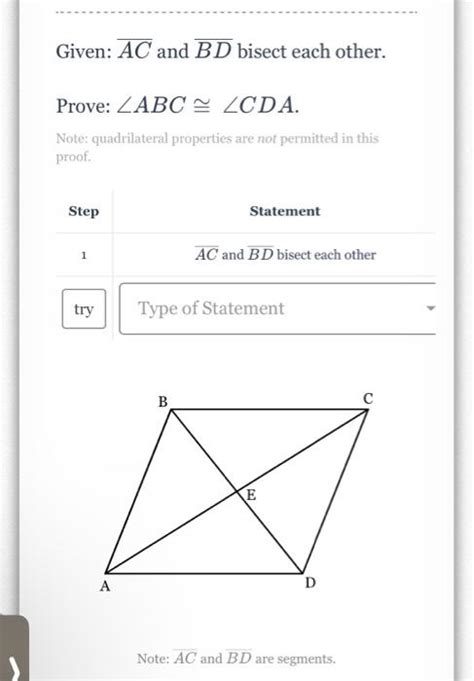
Table of Contents
AC and BD Bisect Each Other: Exploring the Geometry
When two line segments, AC and BD, bisect each other, it signifies a powerful geometric relationship with significant implications. This means that the point of intersection divides both segments into two equal halves. This seemingly simple condition leads to several interesting properties and theorems, especially within the context of quadrilaterals and their various types. This article will delve deep into the ramifications of this bisecting relationship, exploring its impact on different geometric figures and offering numerous illustrative examples.
Understanding Bisection
Before we delve into the complexities of intersecting bisectors, let's establish a clear understanding of the term "bisect." To bisect something means to divide it into two equal parts. In the context of line segments AC and BD, the statement "AC and BD bisect each other" means that the intersection point, let's call it O, divides AC into AO and OC, and BD into BO and OD, such that:
- AO = OC
- BO = OD
This seemingly simple statement opens a door to a world of geometric deductions and proofs.
Implications for Quadrilaterals
The impact of mutually bisecting diagonals is most prominently felt in the properties of quadrilaterals. Different types of quadrilaterals exhibit varying characteristics when their diagonals bisect each other.
Parallelograms: The Hallmark of Mutual Bisection
Perhaps the most significant implication of mutually bisecting diagonals is found in parallelograms. A parallelogram is a quadrilateral where opposite sides are parallel. A crucial and defining property of parallelograms is that their diagonals always bisect each other. This is not just a coincidence; it's a fundamental characteristic that forms the basis for many parallelogram theorems and proofs. This property can be used as a test: if the diagonals of a quadrilateral bisect each other, then the quadrilateral is a parallelogram.
Proof: Consider a quadrilateral ABCD where diagonals AC and BD intersect at point O, such that AO = OC and BO = OD. We can use congruent triangles to prove that opposite sides are parallel. For example, triangles AOB and COD are congruent by SAS (Side-Angle-Side), leading to AB being parallel and equal to CD. Similarly, we can prove that BC is parallel and equal to AD.
Rhombuses and Rectangles: Special Cases of Parallelograms
Rhombuses and rectangles are special types of parallelograms, inheriting the property of mutually bisecting diagonals. However, they add additional constraints.
-
Rhombus: A rhombus is a parallelogram with all four sides equal in length. While the diagonals bisect each other (as in all parallelograms), they also bisect each other at right angles. This perpendicular bisection is a unique property of rhombuses.
-
Rectangle: A rectangle is a parallelogram with four right angles. The diagonals of a rectangle still bisect each other, but they are also equal in length. This equality of diagonal lengths distinguishes rectangles from other parallelograms.
Squares: The Intersection of Rhombus and Rectangle
A square is a special case where it is both a rhombus and a rectangle. Therefore, it inherits all the properties of both: its diagonals bisect each other, bisect each other at right angles, and are equal in length.
Other Quadrilaterals
Not all quadrilaterals have diagonals that bisect each other. For instance, in a trapezoid or a general quadrilateral, the diagonals typically do not bisect each other. The property of mutually bisecting diagonals acts as a distinguishing feature, separating parallelograms and their specialized forms from other quadrilateral types.
Applications and Problem Solving
The property of mutually bisecting diagonals is a cornerstone in numerous geometric problems and applications. Let's explore some examples:
Example 1: Proving a Parallelogram
Suppose you have a quadrilateral ABCD with coordinates A(1,2), B(4,3), C(5,6), and D(2,5). By calculating the midpoint of the diagonals AC and BD, you can check if they coincide. If the midpoints are the same, it proves that the diagonals bisect each other, thus demonstrating that ABCD is a parallelogram.
Example 2: Finding the Length of a Diagonal
Given a parallelogram ABCD where the diagonals bisect each other at point O, and AO = 5 cm, you know that AC = 10 cm. Similarly, if BO = 3 cm, then BD = 6 cm. This demonstrates how the bisection property allows us to easily calculate the lengths of the diagonals.
Example 3: Coordinate Geometry Applications
The concept of bisecting diagonals is extensively used in coordinate geometry to prove properties of quadrilaterals or to find the coordinates of intersection points. Many problems involve finding the equation of a line that passes through the intersection point of the diagonals.
Example 4: Constructing Geometric Figures
Using compasses and straightedges, the property of mutually bisecting diagonals can be used to accurately construct various parallelograms and related shapes. This is a fundamental technique in geometric constructions.
Example 5: Vector Geometry
In vector geometry, the property of mutually bisecting diagonals is crucial when expressing vectors in relation to the vertices and the intersection point of the diagonals. Vector addition and subtraction are simplified considerably.
Advanced Concepts and Extensions
The concept of mutually bisecting diagonals extends beyond simple quadrilaterals. Consider these advanced aspects:
-
Three-Dimensional Geometry: The concept of bisection applies equally well to three-dimensional shapes. Imagine a parallelepiped (a three-dimensional parallelogram); its space diagonals bisect each other.
-
Projective Geometry: In projective geometry, the concept of bisection and intersecting lines takes on a broader perspective, including concepts of infinity and vanishing points.
-
Affine Geometry: In affine geometry, the properties of bisection and parallelism are preserved under affine transformations, which are more general than rigid motions.
-
Non-Euclidean Geometry: The concept of bisection can also be explored in non-Euclidean geometries, although the properties might differ from those in Euclidean geometry.
Conclusion
The seemingly simple statement that "AC and BD bisect each other" holds a wealth of geometric significance. It's a fundamental property that underpins numerous theorems and proofs relating to quadrilaterals, coordinate geometry, vector geometry, and various advanced geometric systems. Understanding this property is essential for anyone delving deeper into the fascinating world of geometry. Its practical applications extend from simple problem-solving to advanced mathematical concepts, making it a cornerstone of geometric understanding. The elegant simplicity of the concept belies its powerful impact across multiple areas of mathematics. Its study allows for a deeper appreciation of the interconnectedness of geometrical ideas and provides a strong foundation for more advanced studies.
Latest Posts
Latest Posts
-
A Denatured Protein Has Lost Its
Apr 04, 2025
-
Difference Between Molecular Weight And Formula Weight
Apr 04, 2025
-
What Is The Common Name For Ch3ch2ch2och2ch2ch3
Apr 04, 2025
-
One Of Chargaffs Rules States That
Apr 04, 2025
-
8 Scientists Who Contributed To The Atomic Theory
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Ac And Bd Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
