Domain And Range Y 1 X
News Leon
Apr 02, 2025 · 7 min read
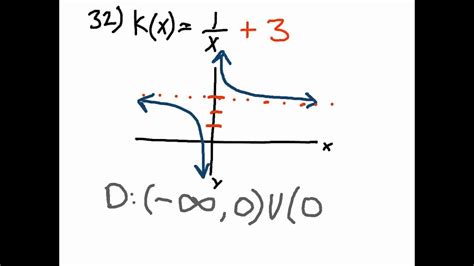
Table of Contents
Domain and Range: Understanding the Heart of a Function
Understanding the domain and range of a function is fundamental to grasping the behavior and properties of that function. These concepts, seemingly simple at first glance, unlock deeper insights into mathematical relationships and are crucial for various applications, from graphing to solving real-world problems. This comprehensive guide will explore domain and range in detail, providing clear definitions, examples, and strategies for determining them for various types of functions.
What is the Domain of a Function?
The domain of a function is the set of all possible input values (often denoted as 'x') for which the function is defined. In simpler terms, it's the set of all x-values that you can "plug into" the function and get a valid, real-number output. The function doesn't "break down" or produce an undefined result for any value within its domain.
Key Considerations for Determining the Domain:
-
Division by Zero: A function is undefined when the denominator of a fraction is zero. Therefore, any values of 'x' that lead to division by zero must be excluded from the domain.
-
Even Roots of Negative Numbers: Even roots (square roots, fourth roots, etc.) are undefined for negative numbers in the real number system. Therefore, you need to ensure the expression inside the even root is non-negative.
-
Logarithms of Non-Positive Numbers: The logarithm of a non-positive number is undefined. The argument of a logarithmic function must always be positive.
-
Other Restrictions: Specific functions may have other restrictions on their input values, which must be considered when determining the domain.
Examples of Finding the Domain:
-
f(x) = 2x + 5: This is a linear function. There are no restrictions on the input 'x'; you can substitute any real number. Therefore, the domain is all real numbers, often written as (-∞, ∞) or ℝ.
-
g(x) = 1/(x - 3): This is a rational function. The denominator cannot be zero, so x - 3 ≠ 0, which means x ≠ 3. The domain is all real numbers except 3, written as (-∞, 3) U (3, ∞).
-
h(x) = √(x + 2): This is a square root function. The expression inside the square root must be non-negative: x + 2 ≥ 0, which implies x ≥ -2. The domain is all real numbers greater than or equal to -2, written as [-2, ∞).
-
k(x) = ln(x - 1): This is a logarithmic function. The argument must be positive: x - 1 > 0, which means x > 1. The domain is all real numbers greater than 1, written as (1, ∞).
-
m(x) = √(4 - x²): This involves a square root and a quadratic expression. We need 4 - x² ≥ 0. This inequality can be solved by factoring: (2 - x)(2 + x) ≥ 0. This inequality holds when -2 ≤ x ≤ 2. The domain is [-2, 2].
What is the Range of a Function?
The range of a function is the set of all possible output values (often denoted as 'y' or 'f(x)') that the function can produce. It's the set of all y-values that the function can "reach" as 'x' varies across its domain.
Determining the Range:
Finding the range can be more challenging than finding the domain. Several techniques can be used:
-
Graphing: The most straightforward method is to graph the function. The range is the set of all y-values covered by the graph.
-
Algebraic Manipulation: Sometimes, you can manipulate the function algebraically to solve for 'x' in terms of 'y' and then determine the restrictions on 'y'.
-
Analyzing the Function Type: Understanding the behavior of different function types (linear, quadratic, exponential, etc.) can help predict the range.
-
Considering Limits and Asymptotes: For functions with asymptotes (lines that the graph approaches but never touches), the asymptotes often define boundaries for the range.
Examples of Finding the Range:
-
f(x) = 2x + 5: This is a linear function. The range is all real numbers, (-∞, ∞) or ℝ, because a line extends infinitely in both the positive and negative y-directions.
-
g(x) = 1/(x - 3): This is a rational function with a vertical asymptote at x = 3. The range is all real numbers except 0, (-∞, 0) U (0, ∞), because the function never equals zero.
-
h(x) = √(x + 2): This is a square root function with a domain of [-2, ∞). The output of a square root is always non-negative. Thus, the range is [0, ∞).
-
k(x) = ln(x - 1): The logarithmic function has a range of all real numbers, (-∞, ∞) or ℝ.
-
m(x) = √(4 - x²): This is a semi-circle with a domain of [-2, 2]. The range is [0, 2]. Because the square root is always non-negative and the maximum value occurs at x = 0, giving a y-value of 2.
Domain and Range in Different Function Types
Let's delve deeper into how domain and range are determined for specific types of functions:
1. Polynomial Functions:
Polynomial functions (e.g., f(x) = x² + 3x - 2) have a domain of all real numbers because there are no restrictions on the input values. The range, however, depends on the degree and coefficients of the polynomial. For example, a quadratic function (degree 2) may have a minimum or maximum value, limiting the range.
2. Rational Functions:
Rational functions are ratios of polynomials (e.g., f(x) = (x + 1)/(x - 2)). The domain excludes values that make the denominator zero. The range depends on the degrees of the numerator and denominator and the presence of horizontal and vertical asymptotes.
3. Radical Functions:
Radical functions involve roots (e.g., f(x) = √x). For even roots, the expression inside the root must be non-negative to have a real-valued output. Odd roots (cube roots, etc.) have a domain of all real numbers. The range depends on the type of root and any other transformations applied to the function.
4. Trigonometric Functions:
Trigonometric functions (sin x, cos x, tan x, etc.) have specific domains and ranges related to the unit circle. For example, sin x and cos x have a range of [-1, 1], while tan x has a range of (-∞, ∞) but an excluded domain at values where cos x = 0 (odd multiples of π/2).
5. Exponential and Logarithmic Functions:
Exponential functions (e.g., f(x) = e<sup>x</sup>) have a domain of all real numbers and a range of (0, ∞). Logarithmic functions (e.g., f(x) = log<sub>b</sub>x) have a domain of (0, ∞) and a range of all real numbers.
Practical Applications of Domain and Range
Understanding domain and range isn't just an abstract mathematical exercise; it has significant practical applications:
-
Modeling Real-World Phenomena: Functions are used extensively to model real-world situations. The domain and range provide important context, defining the realistic limits of the model. For instance, a function modeling the population of a city wouldn't have negative values in its range.
-
Data Analysis and Interpretation: When analyzing data, the domain and range help identify the extent of the data and any potential outliers or unusual values.
-
Computer Graphics and Game Development: Functions are fundamental to computer graphics and game development. Understanding domain and range is crucial for creating realistic images and simulations.
Conclusion: Mastering Domain and Range
Mastering the concepts of domain and range is a cornerstone of function analysis. By understanding how to determine the domain and range for different function types, you gain a deeper understanding of the function's behavior, its limitations, and its potential applications. This knowledge is not only essential for academic success in mathematics and related fields but also invaluable for solving real-world problems and utilizing functions effectively in various contexts. Remember to practice regularly and apply these concepts to diverse examples to solidify your understanding. The ability to confidently and accurately determine the domain and range is a testament to a strong grasp of fundamental mathematical concepts.
Latest Posts
Latest Posts
-
Which Of The Following Substances Should Not Be Filtered
Apr 03, 2025
-
What Type Of Bond Links Amino Acids Together
Apr 03, 2025
-
Auxins Promote The Growth Of The Stem By
Apr 03, 2025
-
Which Of The Following Alcohols Dehydrates With The Fastest Rate
Apr 03, 2025
-
Find The Area Of The Triangle Shown Below
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Domain And Range Y 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
