Find The Area Of The Triangle Shown Below.
News Leon
Apr 03, 2025 · 6 min read
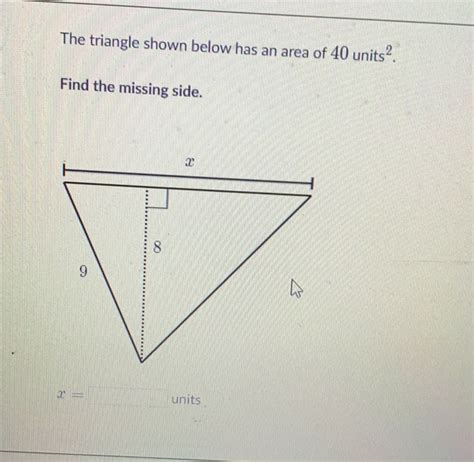
Table of Contents
Find the Area of the Triangle Shown Below: A Comprehensive Guide
Finding the area of a triangle might seem like a simple task, especially from the geometry lessons of our youth. However, the complexity increases significantly when we move beyond basic right-angled triangles and delve into various types, including obtuse, acute, and scalene triangles presented in diverse forms. This comprehensive guide will equip you with multiple methods to accurately calculate the area of a triangle, regardless of its type or the information provided. We'll cover everything from the fundamental formula to advanced techniques, ensuring you're well-prepared to tackle any triangular area problem.
Understanding the Fundamentals: The Basic Formula
The most common and widely known formula for calculating the area of a triangle is:
Area = (1/2) * base * height
This formula is straightforward and works perfectly when you know the length of the base and the corresponding height of the triangle. The base is simply any side of the triangle, and the height is the perpendicular distance from the base to the opposite vertex (the highest point).
Example: A triangle has a base of 6 cm and a height of 4 cm. Its area is (1/2) * 6 cm * 4 cm = 12 cm².
When the Height Isn't Directly Given
The challenge often arises when the height isn't explicitly provided. In such cases, we need to employ alternative methods using other parameters of the triangle.
Advanced Techniques: Beyond the Basic Formula
Let's explore several advanced methods to determine the area of a triangle when the height is unknown:
1. Heron's Formula: Using the Triangle's Sides
Heron's formula is incredibly useful when you know the lengths of all three sides (a, b, and c) of the triangle. It doesn't require the height. The formula involves calculating the semi-perimeter (s) first:
s = (a + b + c) / 2
Then, the area (A) is calculated as:
A = √[s(s-a)(s-b)(s-c)]
Example: Consider a triangle with sides a = 5 cm, b = 6 cm, and c = 7 cm.
- Calculate the semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
- Apply Heron's formula: A = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
Heron's formula is particularly useful for triangles where the height is difficult or impossible to determine directly.
2. Using Trigonometry: When Angles are Known
Trigonometry provides another powerful approach, especially when you know at least one angle and the lengths of two sides. There are several trigonometric formulas applicable depending on the information available.
a) Area = (1/2)ab sin(C)
This formula is highly versatile. Here, 'a' and 'b' are the lengths of two sides, and 'C' is the angle between them.
Example: A triangle has sides a = 8 cm and b = 10 cm, with an included angle C = 30°.
Area = (1/2) * 8 cm * 10 cm * sin(30°) = 20 cm²
b) Area using sine rule and known sides and angle
If we have two sides (a and b) and the angle between them (C) the area can be found using the following formula:
Area = (1/2)ab sinC
This formula allows for the computation of the area using trigonometric functions.
c) Area when we know one side and two angles
In this case, we can use the sine rule to find the other side, then use one of the previous methods to find the area.
3. Coordinate Geometry: Using Vertex Coordinates
If the vertices of the triangle are given as coordinates (x₁, y₁), (x₂, y₂), and (x₃, y₃) on a Cartesian plane, we can use the determinant method to find the area. The formula is:
Area = (1/2) |(x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂))|
The absolute value ensures a positive area.
Example: A triangle has vertices A(1, 1), B(4, 2), and C(2, 5).
Area = (1/2) |(1(2 - 5) + 4(5 - 1) + 2(1 - 2))| = (1/2) |(-3 + 16 - 2)| = (1/2) * 11 = 5.5 square units.
4. Using the R-inradius relationship**
The inradius (r) of a triangle is the radius of the inscribed circle. The area (A) of the triangle can be calculated using the following formula, where s is the semi-perimeter and r is the inradius:
Area = rs
5. Using the Circumradius relationship**
The circumradius (R) is the radius of the circumscribed circle. The area (A) of a triangle can be calculated as follows where a, b, and c are the lengths of the sides, and R is the circumradius:
Area = abc / 4R
Choosing the Right Method: A Practical Guide
The best method to use depends entirely on the information available:
- Base and Height: Use the basic formula (1/2) * base * height. This is the simplest and most direct approach.
- Three Sides: Employ Heron's formula. This is ideal when only side lengths are known.
- Two Sides and Included Angle: Use the trigonometric formula (1/2)ab sin(C).
- Coordinates of Vertices: Utilize the determinant method. This is particularly useful when dealing with triangles plotted on a coordinate plane.
Dealing with Complex Scenarios: Addressing Challenges
Certain scenarios may present additional complexities:
- Triangles within Triangles: Break down the complex shape into smaller, simpler triangles. Calculate the area of each smaller triangle and sum them up.
- Irregular Shapes: Approximate the irregular shape using triangles. The accuracy depends on the number of triangles used. The more triangles used, the more accurate the approximation.
- Triangles with Missing Information: Consider whether you can use geometry principles (such as similar triangles, Pythagorean theorem) to find the missing information before applying an area formula.
Practical Applications: Where Triangular Area Calculations Matter
Calculating the area of a triangle is not just a mathematical exercise; it finds numerous real-world applications across various fields:
- Surveying: Determining land area for property valuation or construction projects.
- Engineering: Calculating structural support needs in bridges, buildings, or other constructions.
- Architecture: Designing and planning building layouts, roof structures, and other components.
- Computer Graphics: Rendering realistic 3D images and modeling complex shapes.
- Physics: Calculating forces and momentum in various scenarios involving triangular structures.
Conclusion: Mastering Triangular Area Calculations
This guide has provided a comprehensive overview of various techniques for finding the area of a triangle. By understanding the different methods and their applications, you'll be well-equipped to tackle a wide range of problems, regardless of the type of triangle or the information provided. Remember to choose the most appropriate method based on the available data, and don't hesitate to break down complex shapes into simpler components if necessary. Mastering these techniques will enhance your problem-solving skills and broaden your understanding of geometry's practical applications in the real world. With practice and a firm grasp of the fundamental principles, calculating the area of any triangle will become a straightforward and manageable task.
Latest Posts
Latest Posts
-
Which Of The Following Is A Non Renewable Source Of Energy
Apr 04, 2025
-
What Binds To The Exposed Cross Bridges On Actin
Apr 04, 2025
-
All Squares Are Rectangles And Rhombuses
Apr 04, 2025
-
What Is The Role Of Toothpaste In Preventing Cavities
Apr 04, 2025
-
Is A Grasshopper A Producer Consumer Or Decomposer
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Find The Area Of The Triangle Shown Below. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
