Why Displacement Is A Vector Quantity
News Leon
Apr 02, 2025 · 5 min read
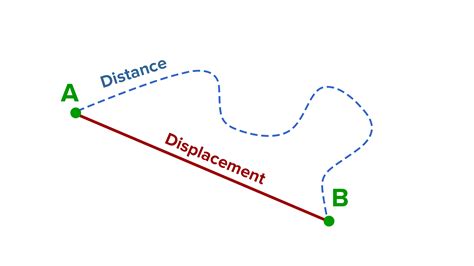
Table of Contents
Why Displacement is a Vector Quantity: A Comprehensive Guide
Displacement, a fundamental concept in physics, often gets confused with distance. While both relate to the separation between two points, their distinct nature stems from the crucial difference: displacement is a vector quantity, while distance is a scalar quantity. This seemingly small distinction has profound implications in understanding motion and solving physics problems. This article delves deep into the reasons why displacement is classified as a vector, exploring its properties and contrasting it with distance.
Understanding Vectors and Scalars
Before diving into the specifics of displacement, let's solidify our understanding of vectors and scalars. These are two fundamental classifications of physical quantities:
-
Scalar Quantities: These quantities are completely described by their magnitude (size or amount). Examples include temperature (30°C), mass (5 kg), speed (20 m/s), and time (10 seconds). They don't possess a direction.
-
Vector Quantities: These quantities require both magnitude and direction to be fully described. Examples include velocity (20 m/s North), force (10 N upwards), acceleration (5 m/s² East), and, crucially for our discussion, displacement. They are often represented graphically as arrows, with the arrow's length representing magnitude and the arrow's direction representing the direction of the quantity.
Defining Displacement
Displacement refers to the change in position of an object. It's the shortest distance between the object's initial and final positions, and crucially, it includes the direction of that change. This inclusion of direction is the defining characteristic that makes it a vector.
Let's consider a simple example. Imagine walking 5 meters East, then 3 meters North. The total distance you've traveled is 8 meters (5 + 3). However, your displacement is not 8 meters. Your displacement is the straight-line distance from your starting point to your ending point, including the direction. Using the Pythagorean theorem, the magnitude of the displacement would be approximately 5.83 meters, and the direction would be a specific angle Northeast (calculated using trigonometry).
This example highlights the key difference: distance considers the entire path taken, while displacement only considers the net change in position.
Why Direction Matters: The Vector Nature of Displacement
The inclusion of direction is not arbitrary; it's essential for accurately representing the change in position. Several aspects demonstrate why direction is critical and why displacement must be treated as a vector:
1. Vector Addition and Subtraction:
Displacement naturally follows the rules of vector addition and subtraction. If you have multiple displacements, the resultant displacement isn't simply the sum of the magnitudes; you need to consider the directions. This is achieved using vector addition methods like the head-to-tail method or component method. Scalar quantities (like distance) cannot be added or subtracted using vector operations.
2. Geometric Representation:
Vectors can be effectively visualized and manipulated geometrically. Displacement vectors can be represented as arrows, allowing for easy understanding of the change in position and the resultant displacement after multiple movements. This visual representation isn't possible with scalar quantities.
3. Applications in Physics:
Many fundamental physics concepts rely on vector quantities, and displacement is no exception. Velocity (rate of change of displacement), acceleration (rate of change of velocity), and force all require both magnitude and direction for proper description and calculation. Treating displacement as a scalar would render many fundamental equations incorrect and severely limit our ability to model physical systems accurately.
4. Relative Displacement:
Displacement is always relative to a reference point or frame. Choosing a different reference point will change the numerical values and potentially even the direction of the displacement. This concept of relative displacement demonstrates the importance of specifying a reference frame, which is a fundamental characteristic of vector quantities.
Contrasting Displacement and Distance: A Detailed Comparison
The following table summarizes the key differences between displacement and distance:
| Feature | Displacement | Distance |
|---|---|---|
| Type | Vector quantity | Scalar quantity |
| Definition | Change in position; shortest distance between initial and final positions, including direction | Total path length traveled |
| Magnitude | Magnitude of the vector | Total path length |
| Direction | Always specified | Not specified |
| Representation | Arrow (magnitude and direction) | Numerical value only |
| Addition | Follows vector addition rules | Simple arithmetic addition |
| Sign | Can be positive, negative, or zero | Always positive |
| Example | 5 meters East | 8 meters (5 meters East + 3 meters North) |
Advanced Concepts and Applications
The vector nature of displacement has profound implications in various advanced physics concepts:
1. Projectile Motion:
Analyzing projectile motion requires a deep understanding of vector components of displacement. Breaking down the displacement vector into horizontal and vertical components allows us to independently analyze the motion in each direction and use vector addition to find the resultant displacement.
2. Relative Motion:
In scenarios involving multiple moving objects, relative displacements help in understanding the motion of one object as observed from another. Vector addition is essential for calculating relative displacements.
3. Circular Motion:
While the instantaneous velocity vector in circular motion is always tangent to the circle, the displacement vector connects the initial and final positions along the arc of the circle. Understanding the relationship between these vectors is essential for analyzing circular motion problems.
4. Multi-dimensional Motion:
In three-dimensional spaces, displacement vectors become essential for accurately representing the change in position of an object moving in all three spatial dimensions (x, y, and z axes).
Conclusion
Displacement is fundamentally a vector quantity because it requires both magnitude and direction for a complete description. Its vector nature is not a mere convention; it's an inherent property that stems from its definition as a change in position. The inclusion of direction is crucial for accurately representing changes in position, performing vector operations, and applying displacement in various physics problems. Understanding this distinction between displacement and distance is key to mastering fundamental physics concepts and solving problems related to motion and mechanics. Ignoring the vector nature of displacement leads to inaccurate calculations and a flawed understanding of the physical world. The consistent application of vector principles ensures correct analysis and a deeper appreciation of how objects move in space.
Latest Posts
Latest Posts
-
What Is The Equivalent Capacitance Of The Four Capacitors
Apr 03, 2025
-
Which Of The Following Is Not A Primary Air Pollutant
Apr 03, 2025
-
Hydrogen Peroxide Is Exposed To Sunlight
Apr 03, 2025
-
Is Nh2 Electron Donating Or Withdrawing
Apr 03, 2025
-
In Two Sentences Describe Your Favorite Meal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Why Displacement Is A Vector Quantity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
