Which One Of The Following Quantities Is A Vector Quantity
News Leon
Mar 31, 2025 · 6 min read
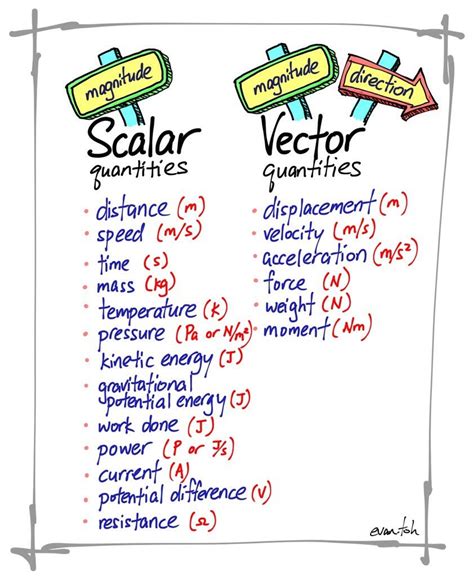
Table of Contents
Which One of the Following Quantities is a Vector Quantity? A Deep Dive into Vectors and Scalars
Understanding the difference between scalar and vector quantities is fundamental in physics and many other scientific fields. While scalars are defined solely by their magnitude (size), vectors possess both magnitude and direction. This article will delve deep into the concept, clarifying the distinction and exploring numerous examples to help you confidently identify vector quantities. We'll also touch upon vector operations and their significance in real-world applications.
What are Scalar Quantities?
Scalar quantities are simple; they only have a magnitude. Think of them as single numbers representing a measurement. Some common examples include:
- Temperature: 25°C, -10°F – these values represent a magnitude of temperature, but there's no direction associated with them.
- Mass: 5 kg, 100 grams – mass is a measure of the amount of matter, regardless of direction.
- Speed: 60 km/h – this tells us how fast something is moving but not where it's moving.
- Energy: 100 Joules – energy is a scalar, describing the capacity to do work, not implying a direction.
- Time: 5 seconds, 2 hours – time progresses regardless of direction.
- Volume: 10 liters, 2 cubic meters – a measure of space, without any directional component.
- Density: 1 g/cm³, 10 kg/m³ – mass per unit volume, a scalar quantity.
- Electric Charge: +2 Coulombs, -1 Coulomb – the magnitude of charge, direction is indicated by the sign.
What are Vector Quantities?
Vector quantities are more complex than scalars; they possess both magnitude and direction. This means that describing a vector requires specifying not only how much (magnitude) but also which way (direction). Representing vectors graphically is often done using arrows, where the arrow's length signifies the magnitude and the arrowhead points in the direction.
Here are some key examples of vector quantities:
- Displacement: This represents the change in position of an object. A displacement of 10 meters east is different from a displacement of 10 meters west, even though the magnitude is the same.
- Velocity: Velocity describes the rate of change of displacement. It's a vector because it includes both speed and direction (e.g., 20 m/s north). Note the difference between speed (scalar) and velocity (vector).
- Acceleration: Acceleration is the rate of change of velocity. A change in either speed or direction, or both, constitutes acceleration. It's a vector quantity because it involves a change in velocity vector.
- Force: Forces have both magnitude (e.g., 10 Newtons) and direction (e.g., upward, downward, left, right, etc.). Forces cause acceleration.
- Momentum: The product of an object's mass and velocity, making it inherently a vector quantity because it depends on the velocity vector.
- Weight: While often confused with mass, weight is actually a vector representing the gravitational force acting on an object. It has both magnitude (weight in Newtons) and direction (always towards the center of the Earth).
- Electric Field: The electric field at a point in space has a magnitude and a direction indicating the force experienced by a unit positive charge at that point.
- Magnetic Field: Similar to the electric field, a magnetic field is described by both magnitude and direction.
Graphical Representation of Vectors
Vectors are commonly represented using arrows. The length of the arrow corresponds to the magnitude of the vector, and the arrowhead indicates the direction. This visual representation greatly aids in understanding and performing vector operations.
Vector Operations: Addition and Subtraction
Unlike scalar operations (simple addition and subtraction), vector operations require considering both magnitude and direction.
Vector Addition
Vector addition is not simply adding the magnitudes. Instead, it involves the parallelogram method or the head-to-tail method.
-
Head-to-Tail Method: Draw the first vector. Then, place the tail of the second vector at the head (arrow tip) of the first vector. The resultant vector (sum) is the vector drawn from the tail of the first vector to the head of the second vector.
-
Parallelogram Method: Draw both vectors originating from the same point. Complete the parallelogram. The resultant vector is the diagonal of the parallelogram, starting from the same origin.
Vector Subtraction
Vector subtraction can be viewed as the addition of the negative of the vector being subtracted. To find the negative of a vector, simply reverse its direction while keeping the magnitude the same.
Examples to Differentiate Scalar and Vector Quantities
Let's consider some scenarios to illustrate the distinction:
Scenario 1: A car travels 60 km/h for 2 hours.
- Speed (60 km/h): Scalar – only magnitude is specified.
- Distance traveled (120 km): Scalar – the total distance is a scalar quantity.
- Displacement (could be 0 km): Vector – this depends on the car's final position relative to its starting point. If the car returns to its origin, the displacement is zero, even though a considerable distance has been covered.
- Velocity: Vector - If the car travels in a straight line, its velocity is 60 km/h in that direction. If the car changes direction, its velocity will change, even if the speed remains constant.
Scenario 2: A ball is thrown upward with a force of 10 Newtons.
- Force (10 N): Vector – it has magnitude and direction (upward).
- Mass of the ball (say 0.5 kg): Scalar – the mass is independent of direction.
- Acceleration (due to gravity): Vector - The acceleration due to gravity is always directed downwards.
- Potential Energy: Scalar - The ball possesses potential energy due to its position, with the magnitude of energy being independent of direction.
Scenario 3: An airplane flies 500 km at a heading of 30 degrees north of east.
- Distance (500 km): Scalar – only the distance traveled is specified.
- Displacement (500 km at 30° N of E): Vector – both magnitude and direction are specified. This defines the airplane's final position relative to its starting point.
- Speed: Scalar - The speed of the plane.
- Velocity: Vector - The velocity of the plane includes both speed and direction.
Practical Applications of Vector Quantities
Understanding vectors is crucial in numerous fields:
- Physics: Describing motion, forces, fields (gravitational, electric, magnetic), momentum, and energy transfer.
- Engineering: Structural analysis (forces on bridges, buildings), fluid mechanics, aerospace engineering (aircraft navigation, trajectory calculation).
- Computer Graphics: Representing positions, directions, movements of objects in 3D space.
- Robotics: Controlling the movement and manipulation of robots.
- Meteorology: Describing wind velocity and direction.
- Navigation: Determining the course and position of ships and aircraft.
- Game Development: Simulating physics, character movement, and projectile trajectories.
Conclusion: Identifying Vector Quantities
To recap, a vector quantity always has both magnitude and direction. Scalars, on the other hand, only have magnitude. Understanding this fundamental difference is critical for accurate scientific descriptions and calculations across various disciplines. Remember to always consider both the magnitude and direction when working with vector quantities. By carefully analyzing the nature of a physical quantity, you can confidently determine whether it is a scalar or a vector. This knowledge is essential for solving problems and understanding phenomena in the physical world.
Latest Posts
Latest Posts
-
Name The Structural And Functional Unit Of All Living Things
Apr 02, 2025
-
Electric Field Of A Cylinder With Uniform Volume Charge Density
Apr 02, 2025
-
The Way Of The World Synopsis
Apr 02, 2025
-
Ba No3 2 Na2so4 Balanced Equation
Apr 02, 2025
-
Which Phase Of Meiosis Separates Homologous Chromosomes
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Which One Of The Following Quantities Is A Vector Quantity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
