Electric Field Of A Cylinder With Uniform Volume Charge Density
News Leon
Apr 02, 2025 · 5 min read
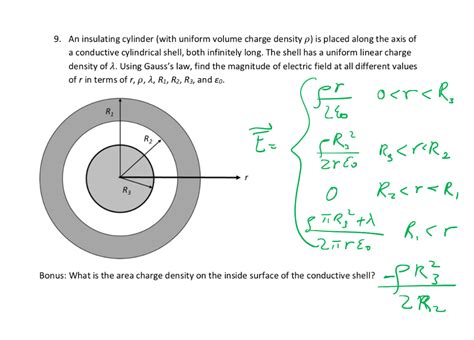
Table of Contents
Electric Field of a Cylinder with Uniform Volume Charge Density: A Comprehensive Guide
The electric field generated by a uniformly charged cylinder is a classic problem in electrostatics with significant applications in various fields, from capacitor design to understanding the behavior of charged particles in plasma physics. This article delves into the detailed calculation and analysis of this electric field, catering to both introductory and advanced learners. We'll explore different approaches, discuss the nuances of the problem, and provide practical insights.
Understanding the Problem: Setting the Stage
We're considering an infinitely long cylinder with a radius 'R' and a uniform volume charge density 'ρ'. This means that the charge is distributed evenly throughout the cylinder's volume. Our goal is to determine the electric field E at any point in space, both inside and outside the cylinder. We'll use Gauss's Law, a powerful tool in electrostatics, to achieve this. Gauss's Law states that the flux of the electric field through a closed surface is proportional to the enclosed charge:
∮ E ⋅ dA = Q<sub>enc</sub> / ε<sub>0</sub>
where:
- E is the electric field vector
- dA is a differential area vector pointing outwards from the Gaussian surface
- Q<sub>enc</sub> is the total charge enclosed within the Gaussian surface
- ε<sub>0</sub> is the permittivity of free space (8.854 x 10<sup>-12</sup> C²/Nm²)
Solving for the Electric Field: Inside the Cylinder (r < R)
To find the electric field inside the cylinder, we construct a cylindrical Gaussian surface with radius 'r' (where r < R) and length 'L', concentric with the charged cylinder. Due to the symmetry of the problem, the electric field will be radial and its magnitude will be constant at any point on the Gaussian surface. Therefore, the dot product in Gauss's Law simplifies:
∮ E ⋅ dA = E ∮ dA = E(2πrL)
Now we need to determine the charge enclosed within our Gaussian surface:
Q<sub>enc</sub> = ρV = ρ(πr²L)
Substituting these into Gauss's Law:
E(2πrL) = ρ(πr²L) / ε<sub>0</sub>
Solving for E, we get the electric field inside the cylinder:
E<sub>inside</sub> = (ρr) / (2ε<sub>0</sub>)
Notice that the electric field inside the cylinder is linearly proportional to the distance 'r' from the cylinder's axis. This means the field strength increases linearly as you move away from the center.
Solving for the Electric Field: Outside the Cylinder (r > R)
For the region outside the cylinder (r > R), we again use Gauss's Law, but this time our cylindrical Gaussian surface has a radius 'r' > R and length 'L'. The enclosed charge now includes the entire charge of the cylinder:
Q<sub>enc</sub> = ρ(πR²L)
The left-hand side of Gauss's Law remains the same as before:
∮ E ⋅ dA = E(2πrL)
Substituting into Gauss's Law:
E(2πrL) = ρ(πR²L) / ε<sub>0</sub>
Solving for E, we obtain the electric field outside the cylinder:
E<sub>outside</sub> = (ρR²) / (2ε<sub>0</sub>r)
Here, the electric field is inversely proportional to the distance 'r' from the cylinder's axis. This is consistent with the electric field of a line charge, reflecting the fact that at large distances, the cylindrical charge distribution appears as a line charge.
Visualizing the Results: A Graphical Representation
The electric field magnitude as a function of the radial distance 'r' can be graphically represented. The graph will show two distinct regions:
- For r < R: A linearly increasing function starting from zero at the center (r=0) and reaching a maximum value at the cylinder's surface (r=R).
- For r > R: A monotonically decreasing function that approaches zero as 'r' tends to infinity.
This visual representation clearly illustrates how the electric field behaves both inside and outside the uniformly charged cylinder. The continuity of the electric field at r=R is also evident.
Applications and Implications
The understanding of the electric field of a uniformly charged cylinder has numerous practical applications:
-
Capacitor Design: Cylindrical capacitors utilize this principle. The electric field calculation helps in determining capacitance and optimizing the design for specific applications.
-
Plasma Physics: Understanding the electric fields in cylindrical geometries is crucial for analyzing the behavior of plasmas confined within cylindrical vessels, such as fusion reactors.
-
Particle Accelerators: The electric fields generated by charged cylindrical structures play a vital role in designing and controlling particle beams in accelerators.
-
Electrostatic Problems: Many electrostatic problems involving cylindrical symmetry can be simplified and solved using the principles discussed here. For example, the calculation of the force on a charged particle placed near such a cylinder.
Limitations and Extensions
While the model of an infinitely long cylinder is useful for simplifying the calculations, it's crucial to acknowledge its limitations:
-
Finite Length Cylinders: For cylinders of finite length, the electric field calculations become more complex, requiring integration techniques to account for the non-uniform charge distribution at the ends.
-
Non-Uniform Charge Density: If the charge density is not uniform, the problem becomes significantly more challenging, often requiring numerical methods for a solution.
-
Dielectric Materials: The presence of dielectric materials surrounding the cylinder significantly affects the electric field, altering the permittivity and requiring modification of Gauss's Law.
These limitations highlight the need for more advanced techniques when dealing with real-world scenarios, which often deviate from the idealized model.
Advanced Concepts and Further Exploration
For a more advanced understanding, one can explore:
-
Potential Difference: Calculating the potential difference between two points in the electric field. This requires integrating the electric field along a path connecting those points.
-
Energy Density: Determining the energy density stored in the electric field of the cylinder, which provides insights into the energy associated with the charge configuration.
-
Numerical Methods: For complex scenarios with non-uniform charge densities or finite cylinder lengths, numerical methods such as finite element analysis (FEA) can provide accurate solutions.
Conclusion
The electric field calculation for a uniformly charged infinite cylinder offers a fundamental understanding of electrostatics. This knowledge provides a cornerstone for tackling more complex problems in various scientific and engineering domains. By understanding the derivations, limitations, and applications discussed here, readers can confidently approach problems involving cylindrical charge distributions and expand their expertise in electromagnetism. Remember, mastering this foundational concept provides a strong base for further explorations into more intricate electrostatic phenomena.
Latest Posts
Latest Posts
-
Which Rule For Assigning Oxidation Numbers Is Correct
Apr 03, 2025
-
Which Of These Characteristics First Developed In Reptiles
Apr 03, 2025
-
Do Annelids Have An Open Or Closed Circulatory System
Apr 03, 2025
-
Which Is Not A Component Of Emotional Intelligence
Apr 03, 2025
-
Arrange The Following Radicals In Order Of Increasing Stability
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of A Cylinder With Uniform Volume Charge Density . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
