Which Of The Following Equations Are Identities
News Leon
Apr 05, 2025 · 5 min read
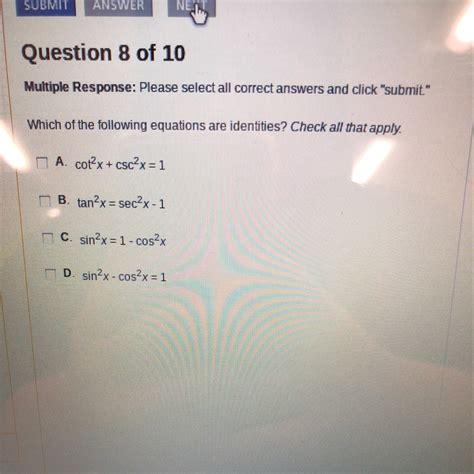
Table of Contents
Which of the Following Equations are Identities? A Deep Dive into Trigonometric and Algebraic Identities
Determining whether an equation is an identity involves verifying if it holds true for all values of its variables within the defined domain. This article explores various techniques for identifying identities, focusing on trigonometric and algebraic examples. We'll delve into the nuances of proving identities, highlighting common pitfalls and offering strategies for successful verification.
Understanding the Concept of an Identity
An identity is an equation that is true for all values of its variables for which both sides of the equation are defined. This differs from a conditional equation, which is only true for specific values of the variables. For example, x + 2 = 5 is a conditional equation (true only when x = 3), while sin²x + cos²x = 1 is an identity (true for all values of x).
Techniques for Proving Identities
Several techniques are employed to prove whether an equation is an identity. These methods often involve manipulating one side of the equation until it matches the other side.
-
Using Fundamental Trigonometric Identities: This approach leverages known trigonometric identities like Pythagorean identities (sin²x + cos²x = 1, 1 + tan²x = sec²x, 1 + cot²x = csc²x), reciprocal identities (sin x = 1/csc x, cos x = 1/sec x, tan x = 1/cot x), and quotient identities (tan x = sin x/cos x, cot x = cos x/sin x). By strategically substituting and simplifying, you can often transform one side of the equation to match the other.
-
Simplifying Expressions: This involves using algebraic manipulation techniques like factoring, expanding brackets, combining like terms, and rationalizing denominators to simplify complex expressions. The goal is to reduce both sides of the equation to their simplest forms to determine if they are equal.
-
Working with Both Sides Simultaneously: In some cases, it can be more efficient to manipulate both sides of the equation simultaneously until they become identical. However, this requires careful attention to ensure each step is reversible.
Examples: Determining if Equations are Identities
Let's analyze several equations to determine whether they represent identities:
1. sin²x + cos²x = 1
This is the fundamental Pythagorean identity. It's true for all values of x. This is an identity. No further proof is needed as this is a foundational identity in trigonometry.
2. tan x = sin x / cos x
This is the quotient identity defining the tangent function. It holds true for all values of x where cos x ≠ 0. This is an identity. The proof relies on the definition of tangent and the relationships between sine and cosine.
3. sec²x - tan²x = 1
This is another Pythagorean identity. We can prove this by starting with the identity sin²x + cos²x = 1. Dividing each term by cos²x (assuming cos x ≠ 0):
(sin²x / cos²x) + (cos²x / cos²x) = 1 / cos²x
This simplifies to:
tan²x + 1 = sec²x
Rearranging, we get:
sec²x - tan²x = 1
This is an identity.
4. sin(x + y) = sin x cos y + cos x sin y
This is the angle sum identity for sine. Proving this identity typically involves using geometric methods or manipulating unit circle definitions. This is beyond the scope of a simple explanation here but it's widely accepted as a fundamental trigonometric identity. This is an identity.
5. (x + 2)² = x² + 4
This is not an identity. Expanding the left side, we get:
(x + 2)² = x² + 4x + 4
This is clearly different from x² + 4. The equation (x + 2)² = x² + 4 is only true when 4x = 0, which means x = 0. Therefore, this is a conditional equation, not an identity.
6. √(x²) = x
This is not an identity. While it's true for positive values of x, it's false for negative values. For example, if x = -2, then √((-2)²) = √4 = 2 ≠ -2. Therefore, this is a conditional equation, not an identity. The correct identity is √(x²) = |x|, where |x| represents the absolute value of x.
7. log(x + y) = log x + log y
This is not an identity. The logarithm of a sum is not equal to the sum of the logarithms. The correct identity involves the logarithm of a product: log(xy) = log x + log y. Therefore, this is not an identity.
8. (a + b)² = a² + 2ab + b²
This is an algebraic identity that arises from expanding the binomial. We can verify this by using the FOIL method (First, Outer, Inner, Last) for expanding the expression:
(a + b)(a + b) = a² + ab + ba + b² = a² + 2ab + b²
This is an identity.
9. a³ - b³ = (a - b)(a² + ab + b²)
This is a difference of cubes factorization. It can be proven by expanding the right side:
(a - b)(a² + ab + b²) = a³ + a²b + ab² - a²b - ab² - b³ = a³ - b³
This is an identity.
10. (a + b)(a - b) = a² - b²
This is the difference of squares factorization. Expanding the left side gives:
(a + b)(a - b) = a² - ab + ab - b² = a² - b²
This is an identity.
Advanced Techniques and Considerations
For more complex identities, particularly those involving multiple trigonometric functions or higher-order polynomials, techniques like:
-
Double Angle Identities: These identities express trigonometric functions of 2x in terms of functions of x (e.g., sin 2x = 2 sin x cos x).
-
Half Angle Identities: These express trigonometric functions of x/2 in terms of functions of x.
-
Sum-to-Product and Product-to-Sum Identities: These identities allow for the conversion between sums/differences of trigonometric functions and products of trigonometric functions.
-
Mathematical Induction: This technique is useful for proving identities that involve sums or sequences.
may be necessary. Remember always to specify the domain for which the identity is valid, as certain identities might not hold true for all real numbers. For example, identities involving tangent and secant are only valid where the cosine is non-zero. Carefully examine the domains of the functions involved to avoid errors.
Conclusion
Determining whether an equation is an identity requires careful analysis and the skillful application of algebraic and trigonometric manipulation techniques. Understanding fundamental identities, employing appropriate simplification strategies, and paying close attention to domains are crucial steps in successfully proving or disproving identities. Through consistent practice and a thorough understanding of the underlying mathematical principles, one can master the art of identity verification. The examples provided here serve as a foundation for exploring more complex identities and developing a deeper appreciation for the elegance and power of mathematical identities.
Latest Posts
Latest Posts
-
The Mrna Strand Is Synthesized In The 5 To 3 Direction
Apr 05, 2025
-
How Many Radians In 60 Degrees
Apr 05, 2025
-
Which Of The Following Is A Strong Base
Apr 05, 2025
-
Part Of The Skull That Encloses The Brain
Apr 05, 2025
-
What Liquid Is Denser Than Water
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Of The Following Equations Are Identities . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
