How Many Radians In 60 Degrees
News Leon
Apr 05, 2025 · 5 min read
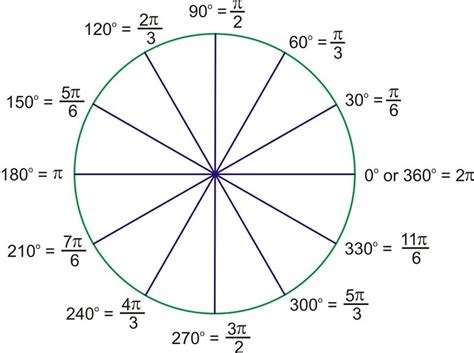
Table of Contents
How Many Radians in 60 Degrees? A Comprehensive Guide
Understanding the relationship between degrees and radians is fundamental in trigonometry and many areas of science and engineering. This comprehensive guide will delve into the conversion process, exploring the underlying concepts and providing practical examples to solidify your understanding of how many radians are in 60 degrees. We'll also explore the broader context of angle measurement and its applications.
Understanding Degrees and Radians
Before diving into the conversion, let's refresh our understanding of degrees and radians. Both are units used to measure angles.
Degrees: The Familiar Unit
Degrees are the more commonly used unit for measuring angles in everyday life. A full circle is divided into 360 degrees (360°). This system likely originates from the Babylonian sexagesimal (base-60) numeral system. The division into 360 degrees provides a convenient number for many geometric and astronomical calculations.
Radians: The Mathematical Standard
Radians, on the other hand, are a more mathematically natural unit for measuring angles. One radian is defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. This definition ties the angle measurement directly to the circle's geometry.
Why Radians are Important: Radians simplify many mathematical formulas, particularly in calculus. Derivatives and integrals of trigonometric functions are significantly simpler when using radians. This makes them the preferred unit in advanced mathematics, physics, and engineering.
Converting Degrees to Radians: The Formula
The conversion between degrees and radians relies on a fundamental relationship: a full circle (360°) is equal to 2π radians. This means that 180° is equal to π radians. This equivalence provides the foundation for our conversion formula:
Radians = (Degrees × π) / 180
This formula allows us to convert any angle measured in degrees into its equivalent in radians.
How Many Radians are in 60 Degrees?
Now, let's apply the formula to answer our core question: How many radians are in 60 degrees?
Using the conversion formula:
Radians = (60° × π) / 180°
Simplifying the fraction:
Radians = π / 3
Therefore, there are π/3 radians in 60 degrees. This is approximately 1.047 radians.
Practical Applications: Why This Conversion Matters
The ability to convert between degrees and radians is crucial in various fields:
Trigonometry:
- Solving Triangles: Many trigonometric functions, like sine, cosine, and tangent, operate most efficiently with radian inputs. Converting angles to radians is essential for accurate calculations in triangle solving.
- Circular Motion: Describing rotational speeds and angular displacements in physics often requires converting between degrees and radians.
- Wave Phenomena: In the study of waves (sound, light, etc.), angles are often expressed in radians because the formulas that govern wave behavior are simpler in this unit.
Calculus:
- Derivatives and Integrals: As mentioned earlier, the derivatives and integrals of trigonometric functions are much cleaner and easier to work with when the angles are expressed in radians. This simplification significantly reduces the complexity of calculations.
- Taylor Series Expansions: The Taylor series expansions of trigonometric functions, widely used in approximations, are based on radians.
Engineering and Computer Science:
- Robotics and Automation: Calculating joint angles in robotic systems often necessitates the use of radians for precise control and movement.
- Computer Graphics: Creating realistic 3D models and animations often requires conversion between degrees and radians for accurate rendering and manipulation of objects.
- Signal Processing: Analyzing and manipulating signals (audio, video) frequently involves trigonometric functions, making radian usage essential.
Beyond 60 Degrees: More Conversion Examples
Let's look at a few more examples to solidify our understanding of the conversion process:
-
Converting 90 Degrees to Radians:
Radians = (90° × π) / 180° = π/2 radians (approximately 1.571 radians)
-
Converting 135 Degrees to Radians:
Radians = (135° × π) / 180° = 3π/4 radians (approximately 2.356 radians)
-
Converting 270 Degrees to Radians:
Radians = (270° × π) / 180° = 3π/2 radians (approximately 4.712 radians)
-
Converting 360 Degrees to Radians:
Radians = (360° × π) / 180° = 2π radians (approximately 6.283 radians) This confirms our initial understanding that a full circle is 2π radians.
Understanding the Unit Circle
The unit circle is a powerful visual tool for understanding the relationship between degrees and radians. A unit circle is a circle with a radius of 1. Marking angles on the unit circle, both in degrees and radians, provides a clear visual representation of the equivalence. The coordinates of points on the unit circle are directly related to the sine and cosine of the corresponding angle. This visualization aids in grasping the concept of radians and their connection to trigonometric functions.
Advanced Applications: Polar Coordinates and Complex Numbers
Radians play a vital role in more advanced mathematical concepts:
- Polar Coordinates: Polar coordinates represent points in a plane using a distance from the origin (radius) and an angle (often expressed in radians). This system is particularly useful for representing circular or spiral shapes.
- Complex Numbers: Complex numbers, represented in polar form, use radians to express the angle of a complex number in the complex plane. This form is essential for calculations involving complex numbers, such as in electrical engineering and quantum mechanics.
Conclusion: Mastering the Radian-Degree Conversion
Understanding how to convert between degrees and radians is a critical skill for anyone working with angles, trigonometry, or related fields. The conversion formula provides a straightforward method for translating between these units. Remember that the π/3 radians in 60 degrees is not just a numerical answer; it represents a fundamental relationship in geometry and mathematics. By grasping this concept and its applications, you'll build a stronger foundation in trigonometry and pave the way for success in more advanced mathematical concepts. The ability to readily convert between degrees and radians will greatly enhance your problem-solving capabilities and comprehension across various disciplines. Through practice and visual aids like the unit circle, you can master this crucial conversion and unlock a deeper understanding of angles and their applications.
Latest Posts
Latest Posts
-
The Spontaneous Overflow Of Powerful Feelings
Apr 06, 2025
-
Pancreatic Juice Does Not Contain
Apr 06, 2025
-
How Far Away Is Pluto In Light Years
Apr 06, 2025
-
Which Element Is Present In All Organic Compounds
Apr 06, 2025
-
If Two Goods Are Substitutes The Cross Price Elasticity Will Be
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about How Many Radians In 60 Degrees . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
