Which Inequality Is Shown In The Graph Below
News Leon
Mar 31, 2025 · 5 min read
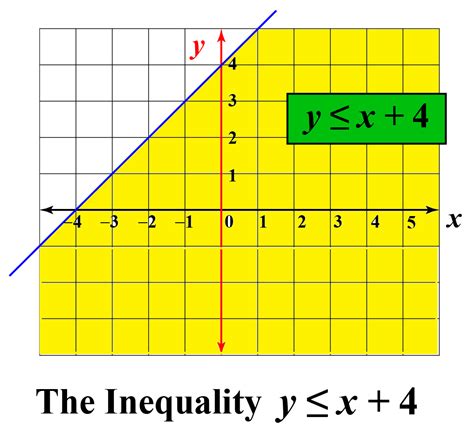
Table of Contents
Decoding Inequality: Analyzing Graphical Representations
This article delves into the art of interpreting graphical representations of inequalities. We'll move beyond simple linear inequalities to explore more complex scenarios, focusing on how to identify the type of inequality shown in a graph, the key features to look for, and how to translate the visual representation into an algebraic expression. We’ll cover various types of inequalities, including linear inequalities in one and two variables, as well as quadratic and absolute value inequalities. Understanding these representations is crucial for success in algebra, calculus, and numerous fields that utilize mathematical modeling.
Understanding the Basics: Symbols and Shading
Before diving into complex graphs, let’s refresh our understanding of inequality symbols and their graphical representations:
-
Less than (<): Represented graphically by a dashed line (or curve) and shading below the line (or to the left of the curve for a one-variable inequality). The line itself is not included in the solution set.
-
Less than or equal to (≤): Represented graphically by a solid line (or curve) and shading below the line (or to the left of the curve for a one-variable inequality). The line itself is included in the solution set.
-
Greater than (>): Represented graphically by a dashed line (or curve) and shading above the line (or to the right of the curve for a one-variable inequality). The line itself is not included in the solution set.
-
Greater than or equal to (≥): Represented graphically by a solid line (or curve) and shading above the line (or to the right of the curve for a one-variable inequality). The line itself is included in the solution set.
Analyzing Linear Inequalities in One Variable
A linear inequality in one variable, such as x < 3, is represented on a number line. The key is to identify the boundary point (3 in this example) and the direction of shading. A circle at the boundary point indicates a strict inequality (< or >), while a filled-in circle indicates an inclusive inequality (≤ or ≥).
Example: A graph showing a filled-in circle at 5 and shading to the left represents the inequality x ≤ 5.
Analyzing Linear Inequalities in Two Variables
Linear inequalities in two variables, such as y > 2x + 1, are represented on a Cartesian plane (x-y coordinate system). The process involves several steps:
-
Identify the Boundary Line: Treat the inequality as an equation (
y = 2x + 1) and graph the line. A dashed line indicates a strict inequality (< or >), while a solid line indicates an inclusive inequality (≤ or ≥). -
Determine the Shaded Region: Choose a test point not on the line (the origin (0,0) is often easiest unless it's on the line). Substitute the coordinates of the test point into the original inequality. If the inequality is true, shade the region containing the test point. If it's false, shade the other region.
Example: To graph y ≤ -x + 4:
-
Graph the line
y = -x + 4as a solid line (because of ≤). -
Test the point (0,0): 0 ≤ -0 + 4 is true. Therefore, shade the region below the line.
Identifying Inequalities from Graphs: A Step-by-Step Approach
Let’s assume we have a graph and we need to determine the inequality it represents. Follow these steps:
-
Identify the type of graph: Is it a number line or a Cartesian plane? This determines the number of variables involved.
-
Examine the boundary line (or point): Is it solid or dashed? A solid line/point indicates an inclusive inequality (≤ or ≥), while a dashed line/point signifies a strict inequality (< or >).
-
Determine the equation of the boundary line (or the value of the boundary point on the number line): Find the slope and y-intercept (for lines on a plane) or simply read the value (for number lines).
-
Identify the shaded region: Determine which side of the line (or point) is shaded. This will determine the direction of the inequality. If shading is above the line, we're dealing with a "greater than" inequality. If it's below, it's "less than."
-
Combine the information: Write the complete inequality using the appropriate symbol.
Beyond Linear Inequalities: Quadratic and Absolute Value Inequalities
Quadratic Inequalities: These inequalities involve quadratic expressions, such as x² - 4x + 3 > 0. Graphically, they're represented by parabolas. The solution set is the region where the parabola is either above (for >) or below (for <) the x-axis. Finding the roots of the quadratic equation (x² - 4x + 3 = 0) helps define the boundary.
Absolute Value Inequalities: Absolute value inequalities, such as |x - 2| < 3, are represented by V-shaped graphs. The solution set is determined by the distance from the vertex of the V-shape. Remember that |x - a| < b means that -b < x - a < b.
Advanced Techniques and Considerations
-
Systems of Inequalities: These involve multiple inequalities graphed on the same coordinate system. The solution to the system is the region where all shaded areas overlap.
-
Non-linear Inequalities: These can include inequalities involving higher-degree polynomials, exponential functions, logarithmic functions, and trigonometric functions. Graphical analysis becomes more complex, often requiring calculus or numerical methods.
-
Contextual Problems: Real-world applications often involve inequalities. Understanding how to interpret the graphs in context is essential. For instance, a graph might represent constraints in a linear programming problem, showing feasible regions for production optimization.
-
Utilizing Technology: Graphing calculators and software packages can greatly assist in visualizing inequalities and determining solution sets, particularly for complex scenarios. They help visualize the regions defined by inequalities and offer a powerful way to check your manual work. However, understanding the fundamental principles remains critical for correct interpretation and avoids reliance on technological solutions alone.
Practicing and Mastering Inequality Interpretation
The key to mastering the interpretation of inequalities is consistent practice. Start with simple linear inequalities, gradually increasing the complexity to include quadratic, absolute value, and systems of inequalities. Focus on understanding the logic behind the graphical representation—the connection between the symbols, the boundary lines, and the shaded regions.
By systematically applying the steps outlined above, and with regular practice, you'll gain proficiency in analyzing and interpreting graphical representations of inequalities. This skill will prove invaluable across various mathematical disciplines and applications. Remember that visualization is a powerful tool in mathematics. The ability to translate between algebraic expressions and graphical representations deepens your understanding and allows you to solve problems more effectively.
Latest Posts
Latest Posts
-
What Is The Aerial Part Of A Plant
Apr 01, 2025
-
A Semipermeable Membrane Is Placed Between
Apr 01, 2025
-
What Are The Two Body Forms Of Cnidarians
Apr 01, 2025
-
Eli The Ice Man Is Used To Remember
Apr 01, 2025
-
Density Of Water At 4 Degree Celsius
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Inequality Is Shown In The Graph Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
