Which Equation Does The Graph Represent
News Leon
Mar 27, 2025 · 6 min read
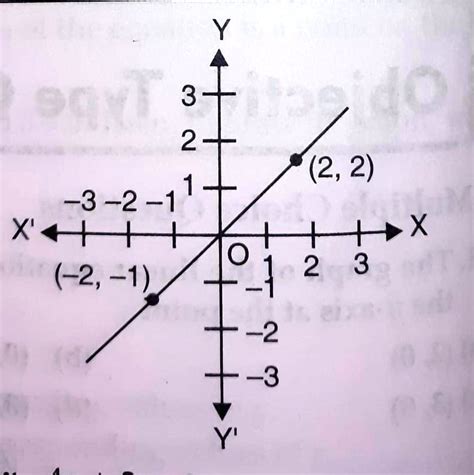
Table of Contents
Which Equation Does the Graph Represent? A Comprehensive Guide
Determining the equation of a graph is a fundamental skill in mathematics and numerous scientific fields. Whether you're dealing with a straight line, a parabola, an exponential curve, or a more complex function, understanding the underlying equation unlocks the ability to predict behavior, model real-world phenomena, and solve problems. This comprehensive guide will equip you with the knowledge and strategies to identify the equation represented by a given graph.
Understanding Different Graph Types and Their Equations
Before diving into the specifics of identifying equations, it's crucial to familiarize ourselves with the common types of graphs and their corresponding equations.
1. Linear Equations: The Straight Line
Linear equations represent straight lines and are characterized by their constant rate of change (slope). The general form of a linear equation is:
y = mx + c
where:
- y is the dependent variable
- x is the independent variable
- m is the slope (representing the rate of change)
- c is the y-intercept (the point where the line intersects the y-axis)
Identifying a linear equation from a graph: Check for a straight line. Determine the slope (m) by calculating the rise over run between two points on the line. The y-intercept (c) is the y-coordinate where the line crosses the y-axis.
2. Quadratic Equations: The Parabola
Quadratic equations represent parabolas, U-shaped curves. The general form of a quadratic equation is:
y = ax² + bx + c
where:
- a, b, and c are constants. The value of 'a' determines the parabola's direction (opens upwards if a > 0, downwards if a < 0) and its width.
Identifying a quadratic equation from a graph: Look for a U-shaped curve. The vertex (the highest or lowest point) can help determine the equation. If you know three points on the parabola, you can substitute their coordinates into the general equation to create a system of equations and solve for a, b, and c.
3. Polynomial Equations: Higher-Order Curves
Polynomial equations represent curves of higher degrees (greater than 2). The general form is:
y = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀
where:
- 'n' is the degree of the polynomial (the highest power of x)
- aₙ, aₙ₋₁, ..., a₁, a₀ are constants.
Identifying a polynomial equation from a graph: Observe the number of turning points (points where the curve changes direction). A polynomial of degree 'n' will have at most (n-1) turning points. Finding several points on the curve and using techniques like polynomial interpolation can help determine the equation.
4. Exponential Equations: Rapid Growth or Decay
Exponential equations represent curves that exhibit rapid growth or decay. The general form is:
y = abˣ or y = a(1 + r)ˣ (for growth) or y = a(1 - r)ˣ (for decay)
where:
- a is the initial value
- b (or 1 + r or 1 - r) is the base, representing the growth or decay factor
- x is the exponent
Identifying an exponential equation from a graph: Look for curves that increase or decrease rapidly. The presence of an asymptote (a line the curve approaches but never touches) is a strong indicator.
5. Logarithmic Equations: Inverse of Exponential
Logarithmic equations represent the inverse relationship of exponential functions. The general form is:
y = logₐ(x)
where:
- a is the base of the logarithm
Identifying a logarithmic equation from a graph: The graph will be a reflection of an exponential graph across the line y = x. It will have a vertical asymptote.
Techniques for Determining the Equation from a Graph
Several techniques can be employed, depending on the type of graph and the information available.
1. Using Key Points and the Slope (Linear Equations)
For linear equations, two points are sufficient to determine the equation. Find the slope (m) using the formula:
m = (y₂ - y₁) / (x₂ - x₁)
Then, use the point-slope form of a linear equation:
y - y₁ = m(x - x₁)
Substitute one of the points and the calculated slope to find the equation.
2. Using the Vertex and Another Point (Quadratic Equations)
For parabolas, the vertex form of a quadratic equation is helpful:
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex. If you know the vertex and another point on the parabola, substitute the coordinates into the equation and solve for 'a'.
3. Using Three Points (Quadratic and Higher-Order Polynomials)
If you have three points for a quadratic, substitute them into the general form y = ax² + bx + c to obtain a system of three equations with three unknowns (a, b, c). Solve this system to find the equation. This method can be extended to higher-degree polynomials, requiring at least n+1 points for a polynomial of degree n.
4. Recognizing Asymptotes and Initial Values (Exponential and Logarithmic Equations)
For exponential and logarithmic functions, look for asymptotes. The asymptote will help determine the general form and potential constants. The initial value (the y-intercept for exponentials, and the x-intercept for logarithms), along with one other point, is typically enough to determine the equation.
Advanced Techniques and Considerations
1. Regression Analysis
For noisy data or complex graphs, regression analysis can be used to find the best-fitting equation. This statistical method involves finding the line or curve that minimizes the distance between the data points and the fitted equation. Software packages like Excel, R, or Python's SciPy library provide tools for performing regression analysis.
2. Graphing Calculators and Software
Graphing calculators and software like GeoGebra, Desmos, or Wolfram Alpha can help to visualize graphs, fit equations, and solve for unknown coefficients.
3. Transforming Non-Linear Relationships into Linear Ones
Sometimes, non-linear relationships can be transformed into linear ones through logarithmic or other mathematical transformations. This allows the use of linear regression techniques for simpler analysis.
4. Contextual Understanding
Always consider the context of the graph. The labels on the axes, the units of measurement, and the overall context of the problem can provide valuable clues in identifying the equation.
Examples
Let's consider some examples to illustrate these techniques:
Example 1: Linear Equation
Suppose a graph shows a straight line passing through points (1, 2) and (3, 6).
- Calculate the slope: m = (6 - 2) / (3 - 1) = 2
- Use the point-slope form: y - 2 = 2(x - 1)
- Simplify: y = 2x
Therefore, the equation is y = 2x.
Example 2: Quadratic Equation
Suppose a graph shows a parabola with vertex (2, 1) and passing through point (3, 3).
- Use the vertex form: y = a(x - 2)² + 1
- Substitute the point (3, 3): 3 = a(3 - 2)² + 1
- Solve for a: a = 2
Therefore, the equation is y = 2(x - 2)² + 1.
By carefully analyzing the graph's characteristics and applying appropriate techniques, you can accurately determine the equation it represents. Remember to always check your work and ensure the equation matches the given graph's features. With practice and a systematic approach, mastering this skill will greatly enhance your mathematical understanding and problem-solving capabilities.
Latest Posts
Latest Posts
-
In Uniform Circular Motion Which Of The Following Is Constant
Mar 30, 2025
-
Why Are Sex Linked Traits More Common In Males Than Females
Mar 30, 2025
-
Difference Between Specific Gravity And Density
Mar 30, 2025
-
Why Did The Pony Express Only Last 18 Months
Mar 30, 2025
-
Which Of The Following Is A True Statement About Vitamins
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Which Equation Does The Graph Represent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
