What Type Of Triangle Is Shown Below
News Leon
Apr 02, 2025 · 5 min read
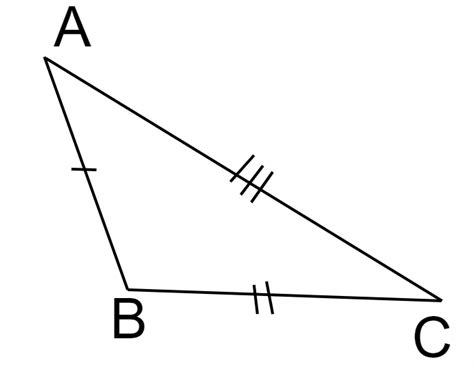
Table of Contents
Decoding Triangles: A Comprehensive Guide to Identifying Triangle Types
Identifying the type of triangle presented in an image or described in a problem requires a deep understanding of the properties that define each category. This guide will explore various triangle classifications based on their sides and angles, providing you with the tools to confidently classify any triangle you encounter. We'll delve into the specifics of equilateral, isosceles, scalene, acute, right, and obtuse triangles, offering numerous examples and practical applications.
Understanding Triangle Classification: Sides and Angles
Triangles, the simplest polygon, are classified based on two key characteristics: the length of their sides and the measure of their angles. Let's break down each classification:
Classifying Triangles by Side Lengths:
-
Equilateral Triangles: These triangles possess the simplest and most symmetrical structure. All three sides are of equal length, resulting in three equal angles as well (each measuring 60 degrees). Think of an equilateral triangle as the perfect, balanced triangle.
- Identifying Feature: Three sides of equal length.
- Angle Property: Three 60-degree angles.
- Example: An equilateral triangle with sides of 5cm each.
-
Isosceles Triangles: This type of triangle features two sides of equal length, known as the legs. The third side, called the base, is of a different length. The angles opposite the equal sides are also equal.
- Identifying Feature: Two sides of equal length.
- Angle Property: Two equal angles.
- Example: A triangle with sides of 4cm, 4cm, and 6cm.
-
Scalene Triangles: These are the most diverse type of triangle, characterized by all three sides having different lengths. Consequently, all three angles also have different measures.
- Identifying Feature: Three sides of unequal lengths.
- Angle Property: Three angles of unequal measure.
- Example: A triangle with sides of 3cm, 5cm, and 7cm.
Classifying Triangles by Angles:
-
Acute Triangles: An acute triangle is defined by having all three angles less than 90 degrees. All equilateral triangles are also acute triangles.
- Identifying Feature: All three angles are less than 90 degrees.
- Example: A triangle with angles of 50, 60, and 70 degrees.
-
Right Triangles: A right triangle is easily recognizable by its single 90-degree angle, often denoted by a small square in the corner. The side opposite the right angle is called the hypotenuse, and it's always the longest side of the triangle. The Pythagorean theorem (a² + b² = c², where a and b are the legs and c is the hypotenuse) is fundamental to solving problems involving right triangles.
- Identifying Feature: One 90-degree angle.
- Example: A triangle with angles of 30, 60, and 90 degrees.
-
Obtuse Triangles: An obtuse triangle contains one angle greater than 90 degrees. This large angle dominates the triangle's shape.
- Identifying Feature: One angle greater than 90 degrees.
- Example: A triangle with angles of 30, 60, and 90 degrees. (Note: This is NOT an obtuse triangle, it's a right triangle. This is a common misconception. To be obtuse, it would need one angle larger than 90 degrees). An example would be a triangle with angles of 20, 40, and 120 degrees.
Combining Classifications: A More Detailed Look
It's crucial to understand that a triangle can be classified using both side lengths and angle measures simultaneously. For instance, a triangle could be an "acute isosceles triangle" or a "right scalene triangle." This dual classification provides a much more precise description of the triangle's characteristics.
Let's explore some examples:
- Acute Isosceles Triangle: This triangle possesses two equal sides and all angles are less than 90 degrees.
- Obtuse Scalene Triangle: This triangle has three unequal sides and one angle greater than 90 degrees.
- Right Isosceles Triangle: This triangle has a 90-degree angle and two equal sides. This is a special case often encountered in geometry problems.
Practical Applications and Real-World Examples
Understanding triangle classifications isn't merely an academic exercise; it has numerous practical applications across various fields:
- Engineering and Construction: Triangles are incredibly strong structures, often used in building bridges, roofs, and other architectural elements. Understanding the properties of different triangle types is crucial for ensuring structural integrity and stability.
- Navigation and Surveying: Trigonometry, which heavily relies on triangle properties, is used in surveying land, calculating distances, and navigation systems (GPS).
- Computer Graphics and Game Development: Triangles are the building blocks of 3D models in computer graphics. Efficiently manipulating and rendering triangles is essential for creating realistic and visually appealing graphics.
- Physics and Mathematics: Triangles play a vital role in various mathematical concepts and physics problems, including calculating forces, vectors, and trajectories.
Solving Problems Involving Triangle Classification
Let's examine some practical problems that require classifying triangles based on their given properties:
Problem 1: A triangle has sides of length 7cm, 7cm, and 10cm. What type of triangle is it?
Solution: Since two sides are equal (7cm, 7cm), this is an isosceles triangle. Because the angles are not explicitly defined, we cannot confirm whether it is also acute, right, or obtuse. Therefore, the most precise classification is an isosceles triangle.
Problem 2: A triangle has angles of 45, 45, and 90 degrees. What type of triangle is it?
Solution: This is a right isosceles triangle. It has one 90-degree angle (right) and two equal angles (isosceles). Its sides are in a specific ratio (1:1:√2).
Problem 3: A triangle has sides of 5cm, 6cm, and 7cm. What type of triangle is it?
Solution: All sides have different lengths, making it a scalene triangle. Since no angles are given, it could be an acute, right, or obtuse scalene triangle. Further information is needed for a more precise classification.
Problem 4: A triangle has angles of 60, 60, and 60 degrees. What type of triangle is it?
Solution: This is an equilateral triangle (and consequently also an acute triangle) because all three angles are equal to 60 degrees, implying all three sides are equal in length.
Conclusion: Mastering Triangle Identification
The ability to correctly identify triangle types is a fundamental skill in mathematics and various applied fields. By understanding the definitions and characteristics of equilateral, isosceles, scalene, acute, right, and obtuse triangles – and the combinations of these classifications – you'll be well-equipped to solve problems, analyze structures, and appreciate the elegance and versatility of these fundamental geometric shapes. Remember to always consider both side lengths and angles when classifying triangles for the most comprehensive and accurate description. This knowledge forms a strong foundation for further exploration in geometry and related disciplines.
Latest Posts
Latest Posts
-
What Is The Equivalent Capacitance Of The Four Capacitors
Apr 03, 2025
-
Which Of The Following Is Not A Primary Air Pollutant
Apr 03, 2025
-
Hydrogen Peroxide Is Exposed To Sunlight
Apr 03, 2025
-
Is Nh2 Electron Donating Or Withdrawing
Apr 03, 2025
-
In Two Sentences Describe Your Favorite Meal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Type Of Triangle Is Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
