What Is The Difference Between A Ray And A Line
News Leon
Apr 04, 2025 · 5 min read
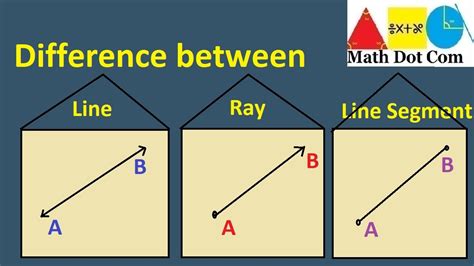
Table of Contents
What's the Difference Between a Ray and a Line? A Deep Dive into Geometric Concepts
Understanding the fundamental differences between geometric concepts like lines and rays is crucial for anyone studying geometry, whether you're a high school student tackling your first geometry lesson or an adult revisiting these concepts for a refresher. While seemingly similar at first glance, lines and rays possess distinct characteristics that define their unique properties and applications within the broader field of mathematics. This article aims to illuminate these differences clearly and comprehensively.
Defining Lines and Rays: Fundamental Characteristics
Before delving into the distinctions, let's establish a firm understanding of each concept:
What is a Line?
A line is a fundamental geometric object defined as a straight, one-dimensional figure extending infinitely in both directions. It has no thickness or width; it's purely a collection of points extending endlessly without any beginning or end. Think of it as a perfectly straight path that goes on forever in opposite directions. Crucially, a line is unbounded, meaning it continues without limitations. We often represent lines using lowercase letters (like line l or line m) or by identifying two points on the line (e.g., line AB).
Key characteristics of a line:
- Infinite extent: Extends infinitely in both directions.
- One-dimensional: Possesses only length; no width or thickness.
- Straight: Follows a perfectly straight path.
- Unbounded: Has no endpoints or boundaries.
- Defined by two points: Any two distinct points uniquely define a line.
What is a Ray?
A ray, in contrast to a line, is a part of a line that starts at a specific point and extends infinitely in only one direction. Imagine shining a flashlight; the beam of light represents a ray – it begins at the bulb (the endpoint) and extends outwards indefinitely. A ray has one endpoint and extends infinitely in the opposite direction. We represent a ray using a lowercase letter and the endpoint, such as ray AB where A is the endpoint, indicating that the ray originates at point A and extends through point B infinitely.
Key characteristics of a ray:
- One endpoint: Has a definite starting point.
- Infinite extent in one direction: Extends infinitely in only one direction from the endpoint.
- One-dimensional: Possesses only length; no width or thickness.
- Straight: Follows a perfectly straight path.
- Bounded at one end: Has a boundary at its endpoint.
- Defined by two points: Requires an endpoint and another point on the ray for definition.
Contrasting Lines and Rays: A Table for Clarity
The following table summarizes the key differences between lines and rays:
| Feature | Line | Ray |
|---|---|---|
| Extent | Infinite in both directions | Infinite in one direction |
| Endpoints | No endpoints | One endpoint |
| Boundaries | Unbounded | Bounded at one end |
| Representation | Line l, Line AB | Ray AB (A is the endpoint) |
| Notation | Often represented with a lowercase letter or two points with a line above (e.g., $\overleftrightarrow{AB}$) | Often represented with a lowercase letter and two points, with an arrow above indicating direction (e.g., $\overrightarrow{AB}$) |
Visual Representations and Examples
Understanding the visual distinction between a line and a ray is paramount. Imagine drawing:
-
A Line: Draw a straight line with arrows on both ends. This visually signifies its infinite extent in both directions. You can't draw the entirety of a line, of course, as it extends infinitely.
-
A Ray: Draw a straight line with an arrowhead at one end and a solid point at the other. The solid point represents the endpoint, and the arrow indicates the direction of infinite extension.
Consider these real-world analogies:
- Line: A perfectly straight, infinitely long highway stretching in both directions.
- Ray: A laser beam emanating from a laser pointer. The laser starts at the pointer and travels infinitely in one direction.
- Line: The horizon viewed from the ocean.
- Ray: Sunlight shining from the sun to the earth.
Advanced Concepts and Applications
The concepts of lines and rays serve as building blocks for more complex geometric ideas. They're fundamental to:
1. Angles:
Angles are formed by two rays sharing a common endpoint (the vertex). The rays are called the sides of the angle. Understanding rays is essential for defining and measuring angles.
2. Line Segments:
A line segment is a part of a line with two defined endpoints. It's a finite portion of a line, unlike a line or a ray which extend infinitely.
3. Coordinate Geometry:
Lines and rays can be represented by equations in coordinate geometry. The equation of a line is typically of the form y = mx + c (where m is the slope and c is the y-intercept). Rays can be expressed with limitations imposed on the domain of the equation, defining the endpoint and the direction of extension.
4. Vector Geometry:
Vectors, which have both magnitude and direction, can be represented using rays. The length of the ray represents the magnitude of the vector, and the direction of the ray represents the direction of the vector.
Common Mistakes and Misconceptions
A common mistake is confusing line segments with rays. While both are parts of a line, a line segment has two defined endpoints, whereas a ray has only one. Another frequent misconception involves the directionality of a ray. Remember, a ray extends infinitely in only one direction from its endpoint.
Conclusion: Mastering the Fundamentals
The distinctions between lines and rays, while subtle, are crucial for a thorough understanding of geometry. By grasping the fundamental differences—infinite extent versus one-directional infinite extent, bounded versus unbounded, and the implications for representing and applying these concepts—you build a strong foundation for more advanced geometric studies. Through careful consideration of definitions, visual representations, and real-world analogies, you can solidify your understanding and successfully navigate the world of geometric figures. Remember to practice visualizing these concepts, as this strengthens your comprehension and allows for a more intuitive grasp of their applications in various mathematical contexts.
Latest Posts
Latest Posts
-
Breakdown Of Glucose To Pyruvic Acid
Apr 04, 2025
-
Are The Following Two Figures Similar Or Congruent
Apr 04, 2025
-
Python Round Number To 2 Decimals
Apr 04, 2025
-
Pepsin Is A Protein Digesting Enzyme Produced By The
Apr 04, 2025
-
An Organ System Is A Group Of Organs That
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Is The Difference Between A Ray And A Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
