Are The Following Two Figures Similar Or Congruent
News Leon
Apr 04, 2025 · 7 min read
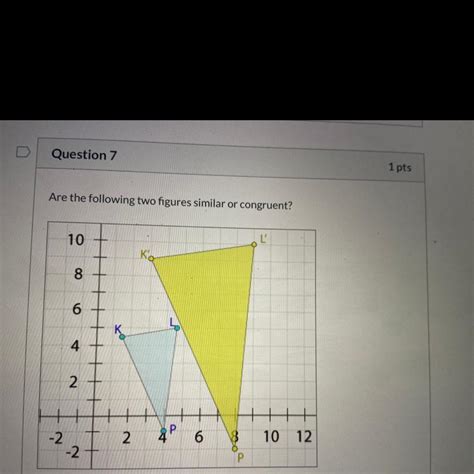
Table of Contents
Are the Following Two Figures Similar or Congruent? A Deep Dive into Geometric Relationships
Determining whether two figures are similar or congruent is a fundamental concept in geometry. While both terms describe relationships between shapes, they represent distinct levels of geometric equivalence. Understanding the nuances of similarity and congruence is crucial for solving various geometric problems and building a strong foundation in mathematics. This comprehensive guide will delve into the definitions of similarity and congruence, explore the criteria for determining each, and provide examples to illustrate the differences and applications of these concepts.
Understanding Similarity
Two figures are similar if they have the same shape but not necessarily the same size. This means that corresponding angles are congruent (equal in measure), and corresponding sides are proportional. Think of enlarging or reducing a photograph – the resulting image is similar to the original; it maintains the same proportions and angles, just on a different scale.
Criteria for Similarity
Several criteria can be used to determine if two figures are similar. The most common are:
-
AA (Angle-Angle) Similarity: If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. Since the sum of angles in a triangle is always 180 degrees, the third angle must also be congruent. This is a powerful criterion because it only requires information about the angles.
-
SSS (Side-Side-Side) Similarity: If the ratios of corresponding sides of two triangles are equal, then the triangles are similar. This means that if the sides of one triangle are proportional to the sides of another triangle, the triangles are similar.
-
SAS (Side-Angle-Side) Similarity: If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar. This combines aspects of both angle and side relationships.
Examples of Similar Figures
Consider two triangles, Triangle A and Triangle B.
-
Example 1 (AA Similarity): If Triangle A has angles of 60°, 60°, and 60°, and Triangle B has angles of 60°, 60°, and 60°, then Triangle A and Triangle B are similar. They are both equilateral triangles.
-
Example 2 (SSS Similarity): Suppose Triangle A has sides of length 3, 4, and 5. Triangle B has sides of length 6, 8, and 10. The ratios of corresponding sides are 3/6 = 4/8 = 5/10 = 1/2. Since the ratios are equal, Triangle A and Triangle B are similar.
-
Example 3 (SAS Similarity): Imagine two triangles with one pair of congruent angles. If the sides adjacent to this angle in both triangles are proportional, then the triangles are similar. For example, if one triangle has sides 4 and 6 adjacent to a 45-degree angle and the other triangle has sides 8 and 12 adjacent to a 45-degree angle, they are similar due to SAS similarity.
It's crucial to remember that similarity is a relationship, not a property of a single figure. A single figure cannot be "similar"; it needs to be compared to another figure to establish a similarity relationship.
Understanding Congruence
Two figures are congruent if they have the same shape and the same size. This implies that corresponding angles and corresponding sides are congruent. Think of two identical stamps – they are congruent; they can be superimposed perfectly on each other.
Criteria for Congruence
Similar to similarity, several criteria determine if two figures are congruent. The most common for triangles are:
-
SSS (Side-Side-Side) Congruence: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
-
SAS (Side-Angle-Side) Congruence: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
-
ASA (Angle-Side-Angle) Congruence: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
-
AAS (Angle-Angle-Side) Congruence: If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
Examples of Congruent Figures
Let's revisit our triangles, Triangle A and Triangle B.
-
Example 1 (SSS Congruence): If Triangle A has sides of length 5, 5, and 5, and Triangle B also has sides of length 5, 5, and 5, then Triangle A and Triangle B are congruent. They are both equilateral triangles of the same size.
-
Example 2 (SAS Congruence): If Triangle A has sides of length 4 and 6 with an included angle of 60°, and Triangle B has sides of length 4 and 6 with an included angle of 60°, then Triangle A and Triangle B are congruent.
-
Example 3 (ASA Congruence): If two angles and the included side of one triangle are equal to two angles and the included side of the other triangle, the triangles are congruent. For example, if both triangles have angles of 30° and 60°, and the side between them has length 7, the triangles are congruent.
Just like similarity, congruence is a relationship between two or more figures. A single figure cannot be declared "congruent" in isolation.
Key Differences Between Similarity and Congruence
The core difference lies in the concept of size.
| Feature | Similarity | Congruence |
|---|---|---|
| Shape | Same | Same |
| Size | Different | Same |
| Angles | Corresponding angles are congruent | Corresponding angles are congruent |
| Sides | Corresponding sides are proportional | Corresponding sides are congruent |
| Scale Factor | Exists (not equal to 1) | Scale factor is 1 |
| Relationship | Indicates proportional relationship | Indicates identical relationship |
Applications of Similarity and Congruence
These geometric concepts have widespread applications across various fields:
-
Architecture and Engineering: Similar and congruent triangles are used extensively in architectural designs, structural analysis, and surveying. Scaling blueprints and ensuring structural integrity rely heavily on these principles.
-
Cartography: Maps utilize similarity to represent large geographical areas on smaller scales. The proportions between distances on the map and the actual distances on Earth maintain the same ratio.
-
Computer Graphics: Computer-aided design (CAD) software utilizes similarity and congruence for creating and manipulating 2D and 3D models. Scaling, rotating, and mirroring objects often involve these concepts.
-
Triangulation: Surveying and navigation techniques frequently employ triangulation, which relies on the principles of similar triangles to measure distances indirectly.
-
Photography: The principles of similar triangles are utilized to explain how perspective works in photography. Distant objects appear smaller in images due to the proportions involved.
Determining Similarity or Congruence: A Step-by-Step Approach
To determine whether two figures are similar or congruent, follow these steps:
-
Identify the Figures: Determine the types of figures you are working with (triangles, quadrilaterals, etc.). Congruence and similarity criteria often vary depending on the shapes.
-
Analyze Angles: Compare the corresponding angles of the two figures. If they are congruent, it suggests potential similarity or congruence.
-
Analyze Sides: Compare the lengths of corresponding sides. If the sides are proportional (ratios are equal), it indicates similarity. If the sides are equal, it indicates congruence.
-
Apply Criteria: Based on the angle and side comparisons, apply the appropriate criteria for similarity (AA, SSS, SAS) or congruence (SSS, SAS, ASA, AAS).
-
Conclusion: Based on your analysis and the applied criteria, determine whether the figures are similar, congruent, or neither.
Advanced Concepts and Considerations
Beyond the basic criteria, more advanced concepts in geometry expand on similarity and congruence:
-
Similar Polygons: The principles of similarity extend beyond triangles to polygons with more than three sides. All corresponding angles must be congruent, and corresponding sides must be proportional.
-
Congruent Polygons: Similar principles apply to congruent polygons, extending beyond triangles.
-
Transformations: Transformations such as translations, rotations, reflections, and dilations can be used to demonstrate similarity and congruence.
By understanding the fundamental principles of similarity and congruence, you can confidently analyze geometric relationships, solve complex problems, and appreciate the mathematical elegance underlying these concepts. The applications of these principles extend far beyond the classroom, impacting various fields and shaping our understanding of the world around us. Remember that consistent practice and a clear understanding of the criteria are essential to mastering this crucial aspect of geometry.
Latest Posts
Latest Posts
-
An Immovable Joint Is Called Synarthrosis Or
Apr 05, 2025
-
Are Viruses Unicellular Or Multicellular Organisms
Apr 05, 2025
-
What Is The Antonym Of Shallow
Apr 05, 2025
-
Which Compound Is A Secondary Amine
Apr 05, 2025
-
Which Of The Statements About Denaturation Are True
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Are The Following Two Figures Similar Or Congruent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
