What Is 8 To The Power Of 5
News Leon
Mar 29, 2025 · 5 min read
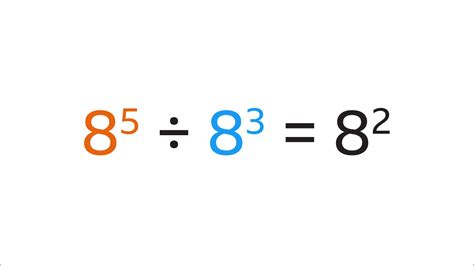
Table of Contents
What is 8 to the Power of 5? A Deep Dive into Exponentiation
The seemingly simple question, "What is 8 to the power of 5?" opens the door to a fascinating exploration of exponentiation, a fundamental concept in mathematics with widespread applications in various fields. This article will not only answer the question directly but will delve into the underlying principles, explore different methods of calculation, and discuss the significance of exponentiation in broader mathematical contexts.
Understanding Exponentiation
Exponentiation, often represented as b<sup>n</sup> (read as "b to the power of n" or "b raised to the power of n"), is a mathematical operation that involves multiplying a base number (b) by itself a specified number of times (n), where 'n' is the exponent. The exponent indicates the number of times the base is used as a factor in the multiplication.
For instance, 2<sup>3</sup> means 2 multiplied by itself three times: 2 x 2 x 2 = 8. In this case, 2 is the base, and 3 is the exponent.
Calculating 8 to the Power of 5
Now, let's tackle the core question: What is 8<sup>5</sup>? This means multiplying 8 by itself five times:
8<sup>5</sup> = 8 x 8 x 8 x 8 x 8
We can calculate this step-by-step:
- 8 x 8 = 64
- 64 x 8 = 512
- 512 x 8 = 4096
- 4096 x 8 = 32768
Therefore, 8 to the power of 5 is 32,768.
Alternative Methods of Calculation
While the step-by-step method is straightforward, other approaches can simplify the calculation, especially for larger exponents.
Using Properties of Exponents
Exponentiation possesses several properties that can streamline calculations. One particularly useful property involves simplifying expressions with exponents of exponents. For example:
(a<sup>m</sup>)<sup>n</sup> = a<sup>m*n</sup>
This means that raising a power to another power is equivalent to multiplying the exponents. We can leverage this property to calculate 8<sup>5</sup> in a different way by expressing 8 as 2<sup>3</sup>:
8<sup>5</sup> = (2<sup>3</sup>)<sup>5</sup> = 2<sup>(3*5)</sup> = 2<sup>15</sup>
Calculating 2<sup>15</sup> is still relatively straightforward, though it may require more steps than the initial method. However, this demonstrates the power of utilizing exponent properties to simplify complex calculations.
Using a Calculator or Computer
For larger exponents or more complex expressions, a calculator or computer software is the most efficient tool. Most calculators have an exponent function (usually denoted by a "^" or "x<sup>y</sup>" symbol). Simply input 8, the exponent symbol, 5, and press "enter" to obtain the result: 32,768.
The Significance of Exponentiation in Mathematics and Beyond
Exponentiation's importance extends far beyond simple calculations. It forms the foundation of many critical mathematical concepts and finds widespread application in various fields.
Exponential Growth and Decay
One of the most significant applications of exponentiation lies in modeling exponential growth and decay. Exponential growth occurs when a quantity increases at a rate proportional to its current value. This phenomenon is observed in various scenarios, including:
- Population growth: The population of a species often exhibits exponential growth under favorable conditions.
- Compound interest: The growth of money invested with compound interest follows an exponential pattern.
- Viral spread: The spread of viral infections or information online can also be modeled using exponential growth.
Conversely, exponential decay describes a quantity decreasing at a rate proportional to its current value. Examples include:
- Radioactive decay: The decay of radioactive materials follows an exponential pattern.
- Drug metabolism: The elimination of drugs from the body often follows an exponential decay model.
Understanding exponential growth and decay is essential in fields like biology, finance, and physics.
Scientific Notation
Exponentiation is crucial in scientific notation, a way of representing extremely large or small numbers concisely. Scientific notation uses powers of 10 to express numbers in the form a x 10<sup>b</sup>, where 'a' is a number between 1 and 10, and 'b' is an integer exponent. This makes it significantly easier to handle numbers of vastly different magnitudes in scientific calculations and data analysis.
Polynomial Functions
Polynomials are expressions involving variables raised to non-negative integer powers. Exponentiation is the fundamental operation that defines these expressions. Polynomials find applications in various areas, including:
- Curve fitting: Polynomials are used to model and approximate data relationships.
- Computer graphics: Polynomials are used in describing curves and surfaces in computer graphics.
- Physics and engineering: Polynomials are used in solving differential equations and modeling various physical phenomena.
Logarithms
Logarithms are the inverse operation of exponentiation. If b<sup>n</sup> = x, then the logarithm base b of x is n (written as log<sub>b</sub>x = n). Logarithms are crucial for solving equations involving exponents and simplifying complex calculations. They are also used extensively in various scientific and engineering disciplines.
Conclusion: Beyond the Calculation
While the answer to "What is 8 to the power of 5?" is 32,768, the true value of this question lies in the broader understanding it unlocks regarding exponentiation. This fundamental mathematical operation underpins many critical concepts across various scientific and practical domains. By grasping the principles of exponentiation and its applications, we gain a deeper appreciation for its importance in mathematics and the world around us. Further exploration of its properties and its relationship with other mathematical concepts will undoubtedly reveal even more about its power and versatility.
Latest Posts
Latest Posts
-
Why Is Dna Replication Called A Semi Conservative Process
Mar 31, 2025
-
Osmosis Involves The Movement Of What Substance
Mar 31, 2025
-
Is 1 3 An Irrational Number
Mar 31, 2025
-
Which Elements Only Have One Valence Electron
Mar 31, 2025
-
Why Is The Testes Located Outside The Body
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 8 To The Power Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
