What Is 6.25 As A Fraction
News Leon
Mar 28, 2025 · 4 min read
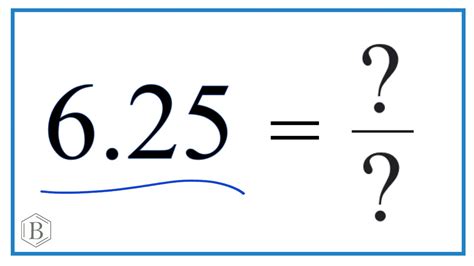
Table of Contents
What is 6.25 as a Fraction? A Comprehensive Guide
Understanding how to convert decimals to fractions is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 6.25 into a fraction but also delve into the underlying principles, providing you with a solid foundation for tackling similar conversions. We'll explore various methods, address common misconceptions, and provide you with practical examples to solidify your understanding. By the end, you'll be confident in converting decimals to fractions, regardless of their complexity.
Understanding Decimals and Fractions
Before we dive into the conversion, let's briefly review the basics of decimals and fractions.
-
Decimals: Decimals represent fractional parts of a whole number using a base-ten system. The digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. For example, in the number 6.25, the '6' represents six whole units, the '2' represents two tenths (2/10), and the '5' represents five hundredths (5/100).
-
Fractions: Fractions represent parts of a whole, expressed as a ratio of two integers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts, while the numerator indicates how many of those parts are being considered. For example, 1/2 represents one out of two equal parts.
Converting 6.25 to a Fraction: Step-by-Step Guide
The conversion of 6.25 to a fraction involves several simple steps:
Step 1: Write the decimal as a fraction with a denominator of 1.
This is the foundational step. We start by placing the decimal number over 1:
6.25/1
Step 2: Multiply both the numerator and the denominator by a power of 10 to eliminate the decimal point.
The key here is to choose a power of 10 (10, 100, 1000, etc.) that will shift the decimal point to the right until it's at the end of the number. In this case, since there are two digits after the decimal point, we multiply by 100:
(6.25 * 100) / (1 * 100) = 625/100
Step 3: Simplify the fraction.
This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. In this case, the GCD of 625 and 100 is 25. Dividing both the numerator and denominator by 25, we get:
625/25 = 25 100/25 = 4
Therefore, the simplified fraction is 25/4.
Alternative Methods for Conversion
While the above method is the most straightforward, there are alternative approaches that can be helpful depending on the specific decimal:
Method 1: Recognizing Common Decimal Equivalents
Some decimals are easily recognizable as common fractions. For instance, 0.25 is 1/4, 0.5 is 1/2, and 0.75 is 3/4. Recognizing these can speed up the conversion process. In the case of 6.25, we can recognize the 0.25 as 1/4. Therefore, 6.25 can be expressed as 6 + 1/4. This can then be converted to an improper fraction by multiplying the whole number (6) by the denominator (4) and adding the numerator (1), keeping the same denominator:
(6 * 4) + 1 = 25 Denominator remains 4
This gives us the same result: 25/4
Method 2: Using the Place Value System
You can also break down the decimal using its place value. 6.25 can be interpreted as:
6 + 2/10 + 5/100
Find a common denominator (in this case, 100):
6 + 20/100 + 5/100 = 6 + 25/100
Then convert the whole number to a fraction with the same denominator:
600/100 + 25/100 = 625/100
Simplify as before to arrive at 25/4.
Converting Improper Fractions to Mixed Numbers
The fraction 25/4 is an improper fraction because the numerator (25) is larger than the denominator (4). To express it as a mixed number (a combination of a whole number and a fraction), we perform a division:
25 ÷ 4 = 6 with a remainder of 1
This means that 25/4 is equal to 6 and 1/4, or 6 1/4. This is equivalent to our original decimal, 6.25.
Practical Applications and Further Exploration
The ability to convert decimals to fractions has numerous applications in various fields:
-
Cooking and Baking: Recipes often require precise measurements, and converting decimal measurements to fractions is crucial for accuracy.
-
Engineering and Construction: Precise calculations in these fields often necessitate the use of fractions for accurate measurements and designs.
-
Finance: Working with percentages and interest rates frequently involves converting decimals to fractions for calculations.
-
Science: Scientific measurements and calculations often involve fractions and decimals, requiring a strong understanding of their interconversion.
Beyond 6.25, you can apply these methods to any decimal. The key is to remember the fundamental principles: write the decimal as a fraction over 1, multiply to eliminate the decimal point, and simplify the resulting fraction. Remember to practice regularly; the more you practice, the more proficient you'll become. You can challenge yourself with more complex decimals, and gradually build your skills to handle even more challenging conversion problems with ease. This understanding of decimal-to-fraction conversion will be a valuable asset throughout your mathematical journey and beyond.
Latest Posts
Latest Posts
-
3x 2y 12 In Slope Intercept Form
Mar 31, 2025
-
Which Type Of Muscle Tissue Is Multinucleated
Mar 31, 2025
-
True Or False Evaporation Is A Physical Change
Mar 31, 2025
-
Do Gram Positive Bacteria Have Porins
Mar 31, 2025
-
Which Of The Following Compounds Is Most Soluble In Water
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is 6.25 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
