The Total Number Of Sides In Two Regular Polygons
News Leon
Apr 03, 2025 · 5 min read
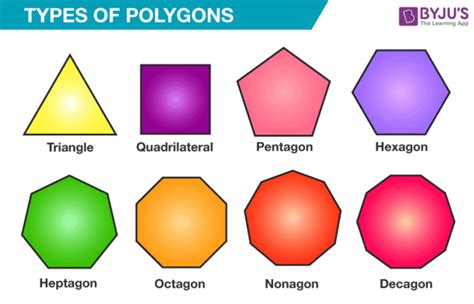
Table of Contents
The Total Number of Sides in Two Regular Polygons: A Deep Dive into Geometry
Understanding the properties of regular polygons is fundamental to geometry. This article explores the intriguing question of determining the total number of sides in two regular polygons, delving into the mathematical concepts and providing practical examples. We'll move beyond simple calculations to explore more complex scenarios and related geometric principles. This in-depth analysis is designed to benefit students, educators, and anyone interested in sharpening their geometric reasoning skills.
Understanding Regular Polygons
Before we delve into calculating the total number of sides, let's establish a clear understanding of what constitutes a regular polygon. A regular polygon is a polygon that is both equiangular (all its angles are equal in measure) and equilateral (all its sides are equal in length). This contrasts with irregular polygons where sides and angles may vary. Common examples of regular polygons include:
- Triangle (3 sides): An equilateral triangle is the simplest regular polygon.
- Square (4 sides): A square is a familiar example with four equal sides and four right angles.
- Pentagon (5 sides): A regular pentagon possesses five equal sides and five equal angles.
- Hexagon (6 sides): A regular hexagon, often found in nature (honeycombs), has six equal sides and angles.
- Heptagon (7 sides): Also known as a septagon.
- Octagon (8 sides): An octagon has eight equal sides and angles.
- Nonagon (9 sides): Also known as an enneagon.
- Decagon (10 sides): A decagon has ten equal sides and angles.
- And so on...
The number of sides directly dictates the properties of a regular polygon. The more sides a polygon has, the closer it approximates a circle.
Calculating the Total Number of Sides: Simple Cases
The most straightforward scenario involves two regular polygons with a known number of sides each. To find the total number of sides, we simply add the number of sides of each polygon.
Example 1:
- Polygon 1: A regular hexagon (6 sides)
- Polygon 2: A regular square (4 sides)
Total number of sides: 6 + 4 = 10 sides
Example 2:
- Polygon 1: A regular pentagon (5 sides)
- Polygon 2: A regular octagon (8 sides)
Total number of sides: 5 + 8 = 13 sides
This simple addition works perfectly when the number of sides for each polygon is explicitly stated. However, real-world problems often require a more nuanced approach.
Calculating the Total Number of Sides: More Complex Scenarios
Let's explore scenarios that require a deeper understanding of geometric relationships and problem-solving strategies.
Scenario 1: Using Relationships between Polygons
Imagine a problem where the number of sides of one polygon is related to the number of sides of the other. For instance:
- Problem: One regular polygon has twice the number of sides as another. The smaller polygon is a regular hexagon. What is the total number of sides in both polygons?
Solution:
- Smaller polygon: A hexagon has 6 sides.
- Larger polygon: It has twice the number of sides, meaning 6 * 2 = 12 sides.
- Total sides: 6 + 12 = 18 sides
Scenario 2: Incorporating Angles
The interior angles of a regular polygon are related to the number of sides. The formula for calculating the measure of each interior angle of a regular polygon with 'n' sides is:
Interior Angle = [(n - 2) * 180°] / n
This formula can be used in problems where the interior angle of a polygon is given, allowing us to determine the number of sides and subsequently the total number of sides in two polygons.
Example:
- Problem: One polygon has an interior angle of 120°. The other polygon has an interior angle of 135°. What is the total number of sides in both polygons?
Solution:
- Polygon 1 (120°): Solving the equation [(n - 2) * 180°] / n = 120° for 'n' yields n = 6 (a hexagon).
- Polygon 2 (135°): Solving the equation [(n - 2) * 180°] / n = 135° for 'n' yields n = 8 (an octagon).
- Total sides: 6 + 8 = 14 sides
Scenario 3: Working with Areas and Perimeters
While less direct, problems might involve the area or perimeter of the polygons. If the side length is known, the perimeter (sum of all sides) can be easily calculated. Relationships between area and side length can also be used, depending on the type of polygon. These more advanced problems require a deeper understanding of geometric formulas and problem-solving skills.
Advanced Concepts and Applications
The concept of calculating the total number of sides extends to more complex areas of geometry and mathematics:
-
Tessellations: Understanding polygon properties is crucial in creating tessellations, where regular polygons fit together without gaps or overlaps. The total number of sides involved in a particular tessellation can be analyzed.
-
Fractals: Fractals often involve the iterative creation of smaller and smaller polygons. The total number of sides at each iteration can be a key element in understanding the fractal's growth and complexity.
-
Computer Graphics: The principles of polygons and their properties are fundamental to computer graphics and 3D modeling. Calculating the total number of sides in complex shapes is important for rendering and efficient computation.
Conclusion: Mastering Polygon Geometry
Calculating the total number of sides in two regular polygons, while seemingly simple in its basic form, opens the door to a deeper appreciation of geometric principles and problem-solving techniques. This article has explored various scenarios, from straightforward addition to more complex problems involving angles, area, and perimeter. By mastering these concepts, you gain a stronger foundation in geometry, laying the groundwork for further exploration of advanced mathematical topics and their applications in diverse fields. Remember to break down complex problems into smaller, manageable steps, and always double-check your calculations to ensure accuracy. The ability to analyze and solve geometric problems is a valuable skill with broad applications in various academic and professional settings.
Latest Posts
Latest Posts
-
Is Drawings A Debit Or Credit
Apr 04, 2025
-
Enzymes Are Catalysts That Increase The Rate Of Reactions By
Apr 04, 2025
-
Does Nitrogen Lose Or Gain Electrons
Apr 04, 2025
-
Able To Be Drawn Into Wire
Apr 04, 2025
-
A Food Chain Starts With A
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about The Total Number Of Sides In Two Regular Polygons . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
