The Product Of Any Two Prime Numbers Is Always Odd
News Leon
Apr 02, 2025 · 5 min read
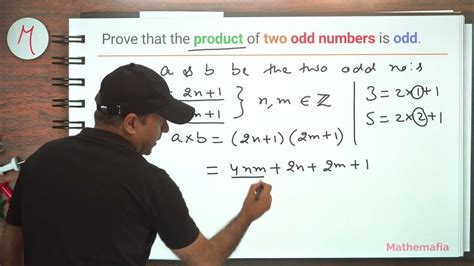
Table of Contents
The Product of Any Two Prime Numbers is Always Odd: A Deep Dive into Prime Numbers and their Properties
The statement "the product of any two prime numbers is always odd" is incorrect. While many prime numbers are odd, the number 2 is also a prime number, and it's even. Therefore, the product of 2 and any other prime number will always be even. This seemingly simple statement highlights a crucial point in understanding prime numbers and their behavior: exceptions exist, and careful analysis is key. This article will delve into the world of prime numbers, exploring their definition, properties, and why the initial statement is false, ultimately providing a deeper understanding of number theory.
Understanding Prime Numbers
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. This seemingly simple definition holds profound implications in mathematics. Prime numbers are the fundamental building blocks of all other integers, a concept formalized by the Fundamental Theorem of Arithmetic. This theorem states that every integer greater than 1 can be represented uniquely as a product of prime numbers, regardless of the order of the factors. This uniqueness is essential in various areas of mathematics, from cryptography to abstract algebra.
Examples of Prime Numbers
The first few prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, and so on. Notice that, except for 2, all these numbers are odd. This observation often leads to the misconception that all prime numbers are odd, but as we've already established, this is incorrect.
The Uniqueness of 2: The Only Even Prime
The number 2 holds a unique position among prime numbers. It's the only even prime number. This is because any even number greater than 2 can be divided by 2, violating the definition of a prime number. All even numbers (except 2) are composite numbers, meaning they have factors other than 1 and themselves. This singular property of 2 significantly impacts the behavior of prime numbers when considered in multiplications and other arithmetic operations.
Why the Statement is False: Counterexamples and Explanation
The assertion that the product of any two prime numbers is always odd is demonstrably false. A simple counterexample suffices to disprove this statement.
Let's consider the prime number 2 and any other prime number, say 3. Their product is 2 * 3 = 6, which is an even number. This single counterexample invalidates the original statement.
Similarly, the product of 2 and 5 is 10 (even), 2 and 7 is 14 (even), 2 and 11 is 22 (even), and so on. In fact, the product of 2 and any prime number will always be even because multiplying any number by 2 results in an even number.
This demonstrates the importance of considering all possibilities when making generalizations in mathematics. A single counterexample is enough to disprove a universal statement.
Exploring the Properties of Prime Number Products
While the product of any two prime numbers isn't always odd, we can analyze the properties of products involving prime numbers in more detail.
Products Involving Only Odd Primes
If we consider only the products of odd prime numbers, the result will always be odd. This is because the product of any two odd numbers is always odd. For example:
- 3 * 5 = 15
- 7 * 11 = 77
- 13 * 17 = 221
This observation highlights a subset of prime number products that consistently yield odd results. However, it's crucial to remember that this applies only when the number 2 is excluded.
Products Involving at Least One Even Prime (2)
As shown earlier, the inclusion of 2 as one of the prime numbers in the product guarantees an even result. This is because multiplying any integer by 2 always results in an even number. The presence of 2, the only even prime, fundamentally alters the outcome.
The Significance of Prime Numbers in Mathematics and Beyond
Prime numbers, despite their seemingly simple definition, play a crucial role in various branches of mathematics and even beyond.
Number Theory
Prime numbers are the cornerstone of number theory, the branch of mathematics dealing with integers and their properties. The distribution of prime numbers, their patterns, and their relationships form the basis for numerous theorems and conjectures, including the famous Riemann Hypothesis, one of the most important unsolved problems in mathematics.
Cryptography
Prime numbers are fundamental to modern cryptography, the science of secure communication. Many encryption algorithms rely on the difficulty of factoring large numbers into their prime components. The difficulty of this process ensures the security of sensitive data transmitted online.
Computer Science
Prime numbers are also important in computer science, particularly in algorithm design and data structure optimization. Efficient algorithms for testing primality and factoring numbers are crucial for various computational tasks.
Other Applications
Beyond these core areas, prime numbers find applications in other fields like physics, chemistry, and even music theory. Their unique properties and the challenges they pose continue to inspire mathematical research and technological advancements.
Conclusion: Accuracy and Precision in Mathematical Statements
The initial statement, "the product of any two prime numbers is always odd," serves as a valuable lesson in the importance of precision and accuracy in mathematical statements. A single counterexample, in this case, the inclusion of the prime number 2, is sufficient to refute a universal claim. This emphasizes the need for careful consideration of all possibilities and the avoidance of hasty generalizations when working with mathematical concepts. Understanding the nuances of prime numbers, especially the unique role of 2, is crucial for a thorough grasp of number theory and its applications. Through rigorous analysis and a focus on detail, we can build a stronger understanding of the fascinating world of prime numbers and their impact on various fields of study. Remember, the beauty of mathematics lies in its precision, and even seemingly simple statements can reveal surprising complexities.
Latest Posts
Latest Posts
-
What Is The Equivalent Capacitance Of The Four Capacitors
Apr 03, 2025
-
Which Of The Following Is Not A Primary Air Pollutant
Apr 03, 2025
-
Hydrogen Peroxide Is Exposed To Sunlight
Apr 03, 2025
-
Is Nh2 Electron Donating Or Withdrawing
Apr 03, 2025
-
In Two Sentences Describe Your Favorite Meal
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about The Product Of Any Two Prime Numbers Is Always Odd . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
